题目内容
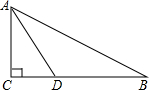 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.(1)在图中作出⊙O;(不写作法,保留作图痕迹)
(2)求证:直线BC为⊙O的切线;
(3)若BD=5,DC=3,求AC的长.
考点:切线的判定,作图—复杂作图
专题:证明题
分析:(1)作AD的垂直平分线交AB于点O,然后以点O为圆心、OA为半径作圆即可;
(2)连结OD,如图1,由AD平分∠BAC得到∠BAD=∠CAD,加上∠OAD=∠ODA,所以∠CAD=∠ODA,则可判断OD∥AC,易得∠ODB=90°,然后根据切线的判定定理得到结论;
(3)先根据平行线分线段成比例定理,由OD∥AC得到
=
=
,则可设BO=5t,AO=3t,所以OD=3t,利用勾股定理得到BD=4t,则有4t=5,解得t=
,所以OD=
,然后证明△BOD∽△BAC,再利用相似比可计算出AC的长.
(2)连结OD,如图1,由AD平分∠BAC得到∠BAD=∠CAD,加上∠OAD=∠ODA,所以∠CAD=∠ODA,则可判断OD∥AC,易得∠ODB=90°,然后根据切线的判定定理得到结论;
(3)先根据平行线分线段成比例定理,由OD∥AC得到
| BO |
| AO |
| BD |
| CD |
| 5 |
| 3 |
| 5 |
| 4 |
| 15 |
| 4 |
解答:(1)解:⊙O为所求,如图,

(2)证明:连结OD,如图1,

∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴直线BC为⊙O的切线;
(3)∵OD∥AC,
∴
=
=
,
设BO=5t,则AO=3t,
∴OD=3t,
在Rt△BOD中,∵BO=5t,OD=3t,
∴BD=
=4t,
∴4t=5,解得t=
∴OD=
,
∵OD∥AC,
∴△BOD∽△BAC,
∴
=
,即
=
,
∴AC=6.

(2)证明:连结OD,如图1,

∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴直线BC为⊙O的切线;
(3)∵OD∥AC,
∴
| BO |
| AO |
| BD |
| CD |
| 5 |
| 3 |
设BO=5t,则AO=3t,
∴OD=3t,
在Rt△BOD中,∵BO=5t,OD=3t,
∴BD=
| OB2-OD2 |
∴4t=5,解得t=
| 5 |
| 4 |
∴OD=
| 15 |
| 4 |
∵OD∥AC,
∴△BOD∽△BAC,
∴
| OD |
| AC |
| BD |
| BC |
| ||
| AC |
| 5 |
| 5+3 |
∴AC=6.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了作图和相似三角形的判定与性质.

练习册系列答案
相关题目
 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/小时)情况,则下列关于车速描述错误的是( )
如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/小时)情况,则下列关于车速描述错误的是( )| A、平均数是23 |
| B、中位数是25 |
| C、众数是30 |
| D、方差是129 |
 如图,在△ABC中,D为AB边上的一点,∠A=36°,AC=BC,AC2=AD•AB.
如图,在△ABC中,D为AB边上的一点,∠A=36°,AC=BC,AC2=AD•AB.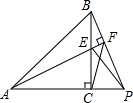 已知△ABC与△ECP为等腰直角三角形,求∠AFC的度数.
已知△ABC与△ECP为等腰直角三角形,求∠AFC的度数. 如图,已知∠C=∠D,∠CAB=∠DBA,AD交BC于点O,请写出图中一组相等的线段
如图,已知∠C=∠D,∠CAB=∠DBA,AD交BC于点O,请写出图中一组相等的线段