题目内容
用配方法和公式法分别解一元二次方程:(x+1)(x-1)+2(x+3)=9.
考点:解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:把原方程整理得x2+2x-4=0;配方法:先移项得到x2+2x=4,再把方程两边都加上1得到x2+2x+1=4+1,即(x+1)2=5,然后利用直接开平方法求解;公式法:先计算出△=22-4×1×(-4)=20,然后代入一元二次方程的求根公式进行计算即可得到方程的解.
解答:解:整理得,x2+2x-4=0
解法一:
∵x2+2x=4,
∴x2+2x+1=4+1,即(x+1)2=5,
∴x+1=±
,
∴x1=-1+
,x2=-1-
;
解法二:
∵△=22-4×1×(-4)=20,
∴x=
=-1±
,
∴x1=-1+
,x2=-1-
.
解法一:
∵x2+2x=4,
∴x2+2x+1=4+1,即(x+1)2=5,
∴x+1=±
| 5 |
∴x1=-1+
| 5 |
| 5 |
解法二:
∵△=22-4×1×(-4)=20,
∴x=
-2±
| ||
| 2×1 |
| 5 |
∴x1=-1+
| 5 |
| 5 |
点评:本题考查了解一元二次方程-配方法:先把方程二次项系数化为1,再把常数项移到方程右边,然后把方程两边加上一次项系数的一半得平方,这样方程左边可写成完全平方式,再利用直接开平方法解方程.也考查了一元二次方程的求根公式.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
在下列方程中,关于x的分式方程的个数有( )
①
=4;②
=4;③
=1;④
=6.
①
| x |
| 5 |
| 6 |
| x |
| x2-9 |
| x+1 |
| 1 |
| x+2 |
| A、2个 | B、3个 | C、4个 | D、1个 |
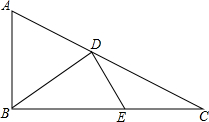 如图,△ABC中,∠ABC=90°,BC=2AB=4,D是AC上一动点,E是BC上一动点,则当BD+DE的值最小时,CE的长为
如图,△ABC中,∠ABC=90°,BC=2AB=4,D是AC上一动点,E是BC上一动点,则当BD+DE的值最小时,CE的长为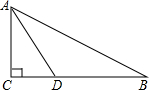 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.