题目内容
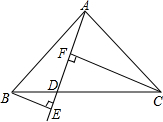 如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.
如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.考点:全等三角形的判定与性质,等腰直角三角形
专题:计算题
分析:CF=BE+EF,理由为:由同角的余角相等得到一对角相等,再由一对直角相等,以及AB=AC,利用AAS得到三角形ABE与三角形CAF全等,利用全等三角形对应边相等得到BE=AF,AE=CF,由AE=AF+EF,等量代换即可得证.
解答:解:CF=BE+EF,理由为:
证明:∵∠BAC=90°,
∴∠BAE+∠CAF=90°,
∵∠BAE+∠ABE=90°,
∴∠CAF=∠ABE,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴CF=AE=AF+EF=BE+EF.
证明:∵∠BAC=90°,
∴∠BAE+∠CAF=90°,
∵∠BAE+∠ABE=90°,
∴∠CAF=∠ABE,
在△ABE和△CAF中,
|
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴CF=AE=AF+EF=BE+EF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在同一直角坐标系中,抛物线y=x2+4x-5与直线y=2x-6的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
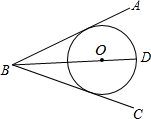 已知O是∠ABC的角平分线BD上的一点,以点O为圆心的⊙O与AB相切,求证:BC与⊙O相切.
已知O是∠ABC的角平分线BD上的一点,以点O为圆心的⊙O与AB相切,求证:BC与⊙O相切.