题目内容
在同一直角坐标系中,抛物线y=x2+4x-5与直线y=2x-6的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:二次函数的性质
专题:计算题
分析:根据两函数的交点问题得到方程组
,再消去y得到关于x的一元二次方程x2+2x+1=0,然后利用判别式确定方程有两个相等的实数解,即方程组有一组解,所以可判断抛物线y=x2+4x-5与直线y=2x-6有一个交点.
|
解答:解:根据题意得
,
消去y得到x2+4x-5=2x-6,
整理得x2+2x+1=0,
因为△=22-4×1=0,方程有两个相等的实数解,
所以方程组有一组解,
所以抛物线y=x2+4x-5与直线y=2x-6有一个交点.
故选B.
|
消去y得到x2+4x-5=2x-6,
整理得x2+2x+1=0,
因为△=22-4×1=0,方程有两个相等的实数解,
所以方程组有一组解,
所以抛物线y=x2+4x-5与直线y=2x-6有一个交点.
故选B.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
点A(5,y1)和B(2,y2)都在直线y=-x上,则y1与y2的关系是( )
| A、y1≥y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、y1>y2 |
数据0、1、2、3的标准差是( )
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
 小敏从A地出发向B地行走,同时小聪从B地出发向 A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间x h之间的关系,则小敏、小聪行走的速度分别是( )
小敏从A地出发向B地行走,同时小聪从B地出发向 A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间x h之间的关系,则小敏、小聪行走的速度分别是( )| A、3m/h和4km/h |
| B、3km/h和3km/h |
| C、4km/h和4km/h |
| D、4km/h和3km/h |
下列变形中,正确的是( )
A、(2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在代数式x2+5,-1,x2-3x+2,π,
,x2+
x2中,单项式有( )
| 5 |
| x |
| 1 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
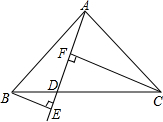 如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.
如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.