题目内容
当|x|≤4时，求|x-2|+|x-3|的最大值和最小值．
考点：绝对值
专题：
分析：利用绝对值的性质，正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0，对x的范围分成-4≤x＜2，2≤x＜3和3≤x≤4共3类，分别对函数解析式化简，然后根据化简结果求得最值．
解答：解：因为-4≤x≤4，所以
当-4≤x＜2时，|x-2|+|x-3|=2-x+3-x=5-2x，
当x=-4时，此时原式最大，原式=5-2×（-4）=13；
当2≤x＜3时，|x-2|+|x-3|=x-2+3-x=1，
当3≤x≤4时，|x-2|+|x-3|=x-2+x-3=2x-5，
当x=4时，此时原式最大，原式=2×4-5=3；
则最大值为13，最小值是：1．
当-4≤x＜2时，|x-2|+|x-3|=2-x+3-x=5-2x，
当x=-4时，此时原式最大，原式=5-2×（-4）=13；
当2≤x＜3时，|x-2|+|x-3|=x-2+3-x=1，
当3≤x≤4时，|x-2|+|x-3|=x-2+x-3=2x-5，
当x=4时，此时原式最大，原式=2×4-5=3；
则最大值为13，最小值是：1．
点评：本题主要考查了绝对值的性质，正确对x的范围进行分类是解决本题的关键．
练习册系列答案
相关题目
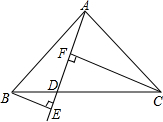如图，画出一个两条直角边相等的Rt△ABC，并过斜边BC上一点D作射线AD，再分别过B，C作射线AD的垂线BE和CF，垂足分别为E，F，量出BE，CF，EF的长，改变D的位置，再重复上面的操作，你是否发现BE，CF，EF的长度之间有某种关系？并证明你的结论．