题目内容
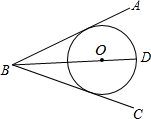已知O是∠ABC的角平分线BD上的一点，以点O为圆心的⊙O与AB相切，求证：BC与⊙O相切．考点：切线的判定,角平分线的性质
专题：证明题
分析：作OE⊥AB于E，OF⊥BC于F，如图，根据切线的性质得到OE为⊙O的半径，再根据角平分线的性质得OE=OF，于是得到OF为⊙O的半径，然后根据切线的判定定理有BC与⊙O相切．
解答：证明：作
OE⊥AB于E，OF⊥BC于F，如图，
∵以点O为圆心的⊙O与AB相切，
∴OE为⊙O的半径，
∵O是∠ABC的角平分线BD上的一点，
∴OE=OF，
即OF为⊙O的半径，
而OF⊥BC，
∴BC与⊙O相切．
OE⊥AB于E，OF⊥BC于F，如图，∵以点O为圆心的⊙O与AB相切，
∴OE为⊙O的半径，
∵O是∠ABC的角平分线BD上的一点，
∴OE=OF，
即OF为⊙O的半径，
而OF⊥BC，
∴BC与⊙O相切．
点评：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了切线的性质和角平分线的性质．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
在代数式x2+5，-1，x2-3x+2，π，
，x2+
x2中，单项式有（ ）
| 5 |
| x |
| 1 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
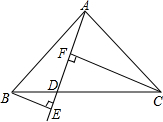如图，画出一个两条直角边相等的Rt△ABC，并过斜边BC上一点D作射线AD，再分别过B，C作射线AD的垂线BE和CF，垂足分别为E，F，量出BE，CF，EF的长，改变D的位置，再重复上面的操作，你是否发现BE，CF，EF的长度之间有某种关系？并证明你的结论．