题目内容
在直角坐标平面上有点A(-1,-2),B(4,2),C(1,c),求c为何值时AC+BC取最小值.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:根据A、B的坐标求得直线AB的解析式,因为当点C(1,c)在直线AB上时AC+BC最小;所以把C代入解析式即可求得.
解答:解:设直线AB的解析式为y=kx+b,
∵A(-1,-2),B(4,2),
∴
,
解得:
.
∴直线AB的解析式为y=
x-
,
当点C(1,c)在直线AB上时AC+BC最小;
∴c=
×1-
=-
.
∵A(-1,-2),B(4,2),
∴
|
解得:
|
∴直线AB的解析式为y=
| 4 |
| 5 |
| 6 |
| 5 |
当点C(1,c)在直线AB上时AC+BC最小;
∴c=
| 4 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
点评:本题考查了轴对称-最短路线问题,待定系数法求解析式.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
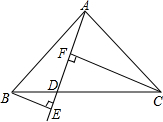 如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.
如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论. 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪AB边的长.
如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪AB边的长.