题目内容
已知抛物线y=x2-kx+2的顶点在坐标轴上，求k的值．
考点：二次函数的性质
专题：
分析：利用顶点的纵坐标列出方程，然后求解即可．
解答：解：当抛物线y=x2-kx+2的顶点在x轴上时，
∵y=0，
∴
=0，
解得k=±2
；
当顶点在y轴上时，-k=0，即k=0．
综上所述，k=±2
或k=0．
∵y=0，
∴
| 4×1×2-(-k)2 |
| 4×1 |
解得k=±2
| 2 |
当顶点在y轴上时，-k=0，即k=0．
综上所述，k=±2
| 2 |
点评：本题考查了二次函数的性质，熟记顶点坐标是解题的关键．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
点A（5，y1）和B（2，y2）都在直线y=-x上，则y1与y2的关系是（ ）
| A、y1≥y2 |
| B、y1=y2 |
| C、y1＜y2 |
| D、y1＞y2 |
在代数式x2+5，-1，x2-3x+2，π，
，x2+
x2中，单项式有（ ）
| 5 |
| x |
| 1 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
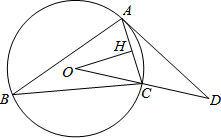已知：如图，△ABC内接于⊙O，OH⊥AC于H，∠B=30°，过A点的直线与OC的延长线交于点D，∠CAD=30°，AD=10
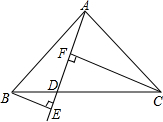如图，画出一个两条直角边相等的Rt△ABC，并过斜边BC上一点D作射线AD，再分别过B，C作射线AD的垂线BE和CF，垂足分别为E，F，量出BE，CF，EF的长，改变D的位置，再重复上面的操作，你是否发现BE，CF，EF的长度之间有某种关系？并证明你的结论．