题目内容
9. 已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.联结AC交EF于点O,延长OC至点M,联结EM、FM.
已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.联结AC交EF于点O,延长OC至点M,联结EM、FM.(1)如果OM=OA,求证:四边形AEMF是菱形;
(2)如果∠MEC=15°,求证:△MEF是等边三角形.
分析 (1)先判定△AEF是等腰三角形,再判定四边形AEMF是平行四边形,即可得出四边形AEMF是菱形;
(2)先根据等腰三角形AEF中,AO垂直平分EF,得出△EFM是等腰三角形,再求得∠FEM=60°,即可得出△MEF是等边三角形.
解答 证明:(1)∵∠BAE=∠DAF,AD=AB,∠D=∠B,
∴Rt△ADF≌Rt△ABE(ASA),
∴AE=AF,即△AEF是等腰三角形,
∵正方形ABCD中,∠BAO=∠DAO=45°,∠BAE=∠DAF,
∴∠EAO=∠FAO,即AO平分∠EAF
∴EO=FO,
又∵OM=OA,
∴四边形AEMF为平行四边形,
又∵AE=AF,
∴四边形AEMF是菱形;
(2)由(1)可知,等腰三角形AEF中,AO垂直平分EF,
∴ME=MF,且∠EOC=90°,
∵正方形ABCD中,∠OCE=45°
∴∠OEC=45°,
∵∠MEC=15°,
∴∠OEM=60°,
∴△MEF是等边三角形.
点评 本题主要考查了菱形的判定与等边三角形的判定,解决问题的关键是运用正方形的性质以及等腰三角形三线合一的性质.在证明题中,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.

练习册系列答案
相关题目
20.一蓄水池有水40m3,如果每分钟放出2m3的水,水池里的水量y(m3)与放水时间t(分)有如下关系:
下列结论中正确的是( )
| 放水时间(分) | 1 | 2 | 3 | 4 | … |
| 水池中水量(m3) | 38 | 36 | 34 | 32 | … |
| A. | y随t的增加而增大 | |
| B. | 放水时为20分钟时,水池中水量为8m3 | |
| C. | y与t之间的关系式为y=40-t | |
| D. | 放水时为18分钟时,水池中水量为4m3 |
4.当0≤x≤3时,一次函数y=-x+3的最大值是( )
| A. | 0 | B. | 3 | C. | -3 | D. | 无法确定 |
1.计算3x2•(-2x)3的结果是( )
| A. | -18x5 | B. | -24x5 | C. | -24x6 | D. | -18x6 |
19.如图1,E为矩形ABCD边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C时停止,点Q从点B出发沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )


| A. | 当t=11s时,y=40cm2 | B. | BE=10cm | ||
| C. | 当0≤t≤10时,y=$\frac{2}{5}$t2 | D. | 当t=16s时,∠PBQ=30° |
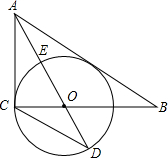 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O. 如图,与∠1构成同位角的是∠B,,与∠2构成同旁内角的是∠1.
如图,与∠1构成同位角的是∠B,,与∠2构成同旁内角的是∠1.