题目内容
6.请你认真阅读下面的小探究系列,完成所提出的问题.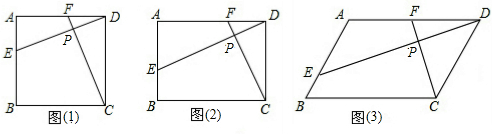
(1)初步探究:如图(1),点E、F分别在正方形ABCD边AB、AD上,DE⊥CF于点P,小芳看到该图后,发现DE=CF,这是因为∠EDA和∠FCD都是∠EDC的余角,就会由ASA判定得出△ADE≌△DCF.
(2)类比发现:小芳进一步思考,如果四边形ABCD是矩形,如图(2),且DE⊥CF于点P,她发现$\frac{DE}{CF}=\frac{AD}{CD}$,请你替她完成证明;
(3)拓展延伸:如图(3),若四边形ABCD是平行四边形,试探究:当∠B与∠EPC满足什么关系时,使得$\frac{DE}{CF}=\frac{AD}{CD}$成立?并证明你的结论.
分析 (2)根据∠A=∠ADC=90°,DE⊥CF,证明∠ADE=∠DCF,得到△ADE∽△DCF,得到答案;
(3)在AD的延长线上取点M,使CM=CF,证明△ADE∽△DCM,得到答案.
解答  (2)证明:∵四边形ABCD是矩形,
(2)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,又∵DE⊥CF,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴$\frac{DE}{CF}$=$\frac{AD}{CD}$;
(3)当∠B+∠EPC=180°时,$\frac{DE}{CF}$=$\frac{AD}{CD}$成立.
证明:在AD的延长线上取点M,使CM=CF,
则∠CMF=∠CFM,
∵AD∥BC,
∴∠CFM=∠FCB,
∵AB∥CD,
∴∠A=∠CDM,又∵∠B+∠EPC=180°,
∴∠AED=∠FCB,
∴∠CMF=∠AED,
∴△ADE∽△DCM,
∴$\frac{DE}{CM}$=$\frac{AD}{CD}$,即$\frac{DE}{CF}$=$\frac{AD}{CD}$.
点评 本题考查的是正方形、矩形和平行四边形的性质,灵活运用三角形全等和相似的判定和性质、正确作出辅助线是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.如果两圆的半径分别为6和4,圆心距为7,那么这两圆的位置关系是( )
| A. | 内含 | B. | 内切 | C. | 相交 | D. | 外切 |
1.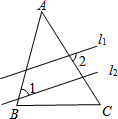 如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
 如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )| A. | 35° | B. | 65° | C. | 85° | D. | 95° |
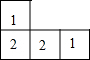 如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )
如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )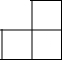

 设实数a、b在数轴上对应位置如图所示,化简:$\sqrt{{a}^{2}}$+|a+b|的结果是b.
设实数a、b在数轴上对应位置如图所示,化简:$\sqrt{{a}^{2}}$+|a+b|的结果是b. 如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=6cm时,BC与⊙A相切.
如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=6cm时,BC与⊙A相切.