题目内容
14．如果两圆的半径分别为6和4，圆心距为7，那么这两圆的位置关系是（ ）| A． | 内含 | B． | 内切 | C． | 相交 | D． | 外切 |
分析 根据数量关系来判断两圆的位置关系．设两圆的半径分别为R和r，且R≥r，圆心距为d：外离，则d＞R+r；外切，则d=R+r；相交，则R-r＜d＜R+r；内切，则d=R-r；内含，则d＜R-r．
解答 解：∵两圆的半径分别是4和6，圆心距为6，
6-4=2，6+4=10，
∴2＜7＜10，
∴两圆相交．
故选C．
点评 本题考查了两圆的位置关系与数量之间的联系，解题的关键是熟知圆的半径与两圆的圆心距之间的关系．
练习册系列答案
相关题目
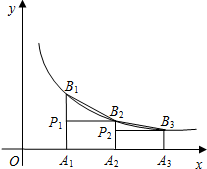如图，已知点A1，A2，A3，…An，…是x轴上的点，且OA1=A1A2=A2A3=…An-1An…=1，分别过点A1，A2，A3，…An，…作x轴的垂线交反比例函数y=$\frac{1}{x}$（x＞0）的图象于点B1，B2，B3，Bn，…，过点B2作B2P1⊥A1B1于点P1，过点B3作B3P2⊥A2B2于点P2…，记△B1P1B2的面积为S1，△B2P2B3的面积为S2…，△BnPnBn+1的面积为Sn，则S1+S2+S2+…+S2015=$\frac{2015}{4032}$．
5．
如图，△ABC的顶点A，B，C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是（ ）
如图，△ABC的顶点A，B，C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是（ ）| A． | 70° | B． | 60° | C． | 45° | D． | 30° |
如图是每个画上都有一个汉字的正方体的一种平面展开图，那么在原正方体中和“国”字相对的面是（ ）
9．若一个关于x的一元二次方程的两个根分别是数据2，4，5，4，3，5，5的众数和中位数，则这个方程是（ ）
| A． | x2-7x+12=0 | B． | x2+7x+12=0 | C． | x2-9x+20=0 | D． | x2+9x+20=0 |
19．若$\sqrt{3x-6}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≥-2 | B． | x≠-2 | C． | x≥2 | D． | x≠2 |
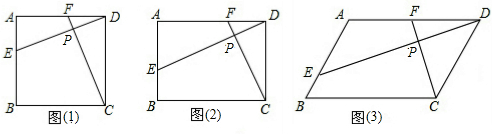
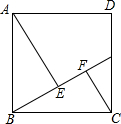如图，正方形ABCD的边长是10，点G是CD边上任意一点，AE⊥BG于点E，CF⊥BG于点F，AE=8．