题目内容
11. 设实数a、b在数轴上对应位置如图所示,化简:$\sqrt{{a}^{2}}$+|a+b|的结果是b.
设实数a、b在数轴上对应位置如图所示,化简:$\sqrt{{a}^{2}}$+|a+b|的结果是b.
分析 首先根据数轴的特征,可得a<0<b,而且a+b>0;然后分别求出$\sqrt{{a}^{2}}$、|a+b|的值是多少,再把它们求和,求出$\sqrt{{a}^{2}}$+|a+b|的结果是多少即可.
解答 解:根据数轴的特征,可得
a<0<b,而且a+b>0,
∴$\sqrt{{a}^{2}}$+|a+b|
=-a+a+b
=b
故答案为:b.
点评 (1)此题主要考查了实数与数轴,要熟练掌握,解答此题的关键是要明确:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
(2)此题还考查了二次根式的性质和化简,注意算术平方根的非负性质,以及绝对值的非负性质的应用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
19.若$\sqrt{3x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≠-2 | C. | x≥2 | D. | x≠2 |
 如图是每个画上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是( )
如图是每个画上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是( )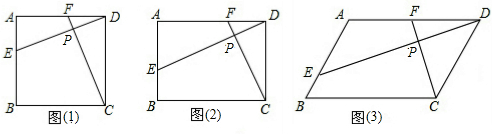
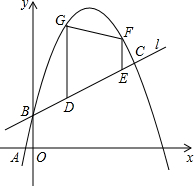 如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).
如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).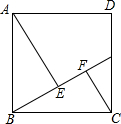 如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.
如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.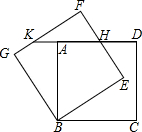 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.