题目内容
16. 如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=6cm时,BC与⊙A相切.
如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=6cm时,BC与⊙A相切.
分析 当BC与⊙A相切,点A到BC的距离等于半径即可.
解答  解:如图,过点A作AD⊥BC于点D.
解:如图,过点A作AD⊥BC于点D.
∵AB=AC,∠B=30°,
∴AD=$\frac{1}{2}$AB,即AB=2AD.
又∵BC与⊙A相切,
∴AD就是圆A的半径,
∴AD=3cm,
则AB=2AD=6cm.
故答案是:6.
点评 本题考查了切线的判定.此题利用了切线的定义和含30度角的直角三角形的性质得到AB的长度的.

练习册系列答案
相关题目
4.如图,在边长为$\sqrt{3}$+1的菱形ABCD中,∠A=60°,点E,F分别在AB,AD上,沿EF折叠菱形,使点A落在BC边上的点G处,且EG⊥BD于点M,则EG的长为$\sqrt{3}$.

11.下列计算结果正确的是( )
| A. | a4•a2=a8 | B. | (a5)2=a7 | C. | (a-b)2=a2-b2 | D. | (ab)2=a2b2 |
8.计算2-1+$\frac{1}{2}$的结果是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 2$\frac{1}{2}$ |
5.某市居民用电的电价实行阶梯收费,收费标准如下表:
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
| 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
| 0<x≤200 | a |
| 200<x≤400 | b |
| x>400 | 0.92 |
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?

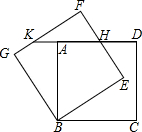 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3. 如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).
如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).