题目内容

1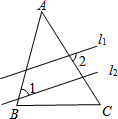．如图，直线l1∥l2，且分别于△ABC的两边AB相交．若∠A=50°，∠1=35°，则∠2的度数为（　　）
A．35°B．65°C．85°D．95°

分析 先根据平行线的性质求出∠3，再根据三角形的内角和定理求出即可．

解答 解：如图：

∵直线l1∥l2，∠1=35°，
∴∠3=∠1=35°，
∵∠A=50°，
∴∠2=180°-∠A-∠3=95°，
故选D．

点评 本题考查了平行线的性质，三角形内角和定理的应用，能求出∠3的度数是解此题的关键，注意：两直线平行，同位角相等．

练习册系列答案
相关题目
11．已知关于x的分式方程$\frac{a+3}{x+1}$=1的解是非正数，则a的取值范围是a≤-2且a≠-3．
12．|-4|的值是（　　）
A．4B．-4C．2D．-2
9．若一个关于x的一元二次方程的两个根分别是数据2，4，5，4，3，5，5的众数和中位数，则这个方程是（　　）
A．x2-7x+12=0B．x2+7x+12=0C．x2-9x+20=0D．x2+9x+20=0
16．估计$\sqrt{8}$-2的值在（　　）
A．0到1之间B．1到2之间C．2到3之间D．3至4之间
6．请你认真阅读下面的小探究系列，完成所提出的问题．

（1）初步探究：如图（1），点E、F分别在正方形ABCD边AB、AD上，DE⊥CF于点P，小芳看到该图后，发现DE=CF，这是因为∠EDA和∠FCD都是∠EDC的余角，就会由ASA判定得出△ADE≌△DCF．
（2）类比发现：小芳进一步思考，如果四边形ABCD是矩形，如图（2），且DE⊥CF于点P，她发现$\frac{DE}{CF}=\frac{AD}{CD}$，请你替她完成证明；
（3）拓展延伸：如图（3），若四边形ABCD是平行四边形，试探究：当∠B与∠EPC满足什么关系时，使得$\frac{DE}{CF}=\frac{AD}{CD}$成立？并证明你的结论．
13．已知x=$\sqrt{2}$，求代数式（$\frac{1}{x-1}$-$\frac{1}{x+1}$）÷$\frac{x}{{x}^{2}-1}$的值．
10．如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．下列结论：①CE=CF；②当AD=2时，EF与半圆相切；③线段EF的最小值为4；④若点F恰好落在BC上，则AD=4．其中正确结论的序号是①②．
11．下列计算结果正确的是（　　）
A．a4•a2=a8B．（a5）2=a7C．（a-b）2=a2-b2D．（ab）2=a2b2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网