题目内容
18.若x-$\frac{1}{x}$=$\frac{1}{2}$,则x2-$\frac{1}{{x}^{2}}$=±$\frac{\sqrt{17}}{4}$.分析 根据完全平方公式,先将原式两边平方,求出x+$\frac{1}{x}$,再根据平方差公式把要求的式子进行变形,代入计算即可.
解答 解:将x-$\frac{1}{x}$=$\frac{1}{2}$两边平方,
可得:${x}^{2}+\frac{1}{{x}^{2}}=2\frac{1}{4}$,
(x+$\frac{1}{x}$)2=x2+2+$\frac{1}{{x}^{2}}$=$\frac{17}{4}$
x+$\frac{1}{x}$=±$\frac{\sqrt{17}}{2}$,
∴x2-$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)(x+$\frac{1}{x}$)=±$\frac{\sqrt{17}}{4}$,
故答案为:±$\frac{\sqrt{17}}{4}$.
点评 本题考查的是完全平方公式和平方差公式的应用,正确把代数式应用完全平方公式和平方差公式进行变形是具体点关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若一个关于x的一元二次方程的两个根分别是数据2,4,5,4,3,5,5的众数和中位数,则这个方程是( )
| A. | x2-7x+12=0 | B. | x2+7x+12=0 | C. | x2-9x+20=0 | D. | x2+9x+20=0 |
8.计算2-1+$\frac{1}{2}$的结果是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 2$\frac{1}{2}$ |
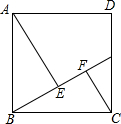 如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.
如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②当AD=2时,EF与半圆相切;③线段EF的最小值为4;④若点F恰好落在BC上,则AD=4.其中正确结论的序号是①②.
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②当AD=2时,EF与半圆相切;③线段EF的最小值为4;④若点F恰好落在BC上,则AD=4.其中正确结论的序号是①②.