题目内容
13.如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A-B-C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)(1)当P在AB上,t=4s时,△APE的面积为长方形面积的$\frac{1}{3}$;
(2)整个运动过程中,t为何值时,△APE为直角三角形?

分析 (1)设t秒后,△APE的面积为长方形面积的$\frac{1}{3}$,根据题意得:△APE的面积=$\frac{1}{2}$AP•AD=$\frac{1}{2}$t×4=$\frac{4×6}{3}$,从而求得t值;
(2)①当P运动到AB中点时△AEP为直角三角形,此时∠APE为直角,t=3;②当P运动到BC上时,∠AEP为直角时利用相似三角形求得PB的长即可求得t值.
解答 解:(1)设t秒后,△APE的面积为长方形面积的$\frac{1}{3}$,
根据题意得:AP=t,
∴△APE的面积=$\frac{1}{2}$AP•AD=$\frac{1}{2}$t×4=$\frac{4×6}{3}$,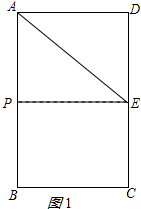
解得:t=4,
∴4秒后,△APE的面积为长方形面积的$\frac{1}{3}$;
(2)①当t=3时,AP=3,如图1所示:
∵E为CD的中点,
∴CE=DE=3,
∵四边形ABCD是矩形,
BC=AD=4,
∴四边形APED是矩形,
∴PE⊥AB,
∴△APE是直角三角形,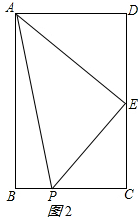
②当P在BC上时,若△APE是直角三角形,∠AED+∠PEC=90°,如图2所示:
∵∠ADE=∠ECP=90°,
∴∠AED=∠EPC,
∴△ADE∽△ECP,
∴$\frac{CP}{DE}$=$\frac{CE}{AD}$,
解得:CP=$\frac{CE•DE}{AD}$=$\frac{3×3}{4}$=$\frac{9}{4}$,
∴PB=BC-PC=4-$\frac{9}{4}$=$\frac{7}{4}$,
∴t=6+$\frac{7}{4}$=$\frac{31}{4}$;
综上所述:当t=3s或t=$\frac{31}{4}$s时,△APE为直角三角形.
点评 本题考查了矩形的性质、直角三角形的判定与性质、三角形面积、动点问题;动点问题更是中考中的热点考题,有一定的难度,解题的关键是能够化动为静,利用直角三角形的性质求解.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案| A. | y=-2x2 | B. | y=-2(x-2)2 | C. | y=-2(x-2)2-10 | D. | y=-2x2-10 |
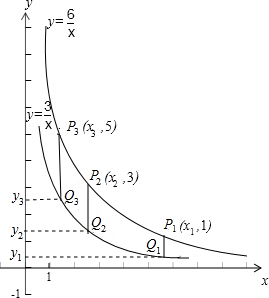 两个反比例函数y=$\frac{3}{x}$,y=$\frac{6}{x}$在第一象限内的图象如图所示,点P1,P2,P3,…,P2015在反比例函数y=$\frac{6}{x}$图象上,它们的横坐标分别是x1,x2,x3,…,x2015,纵坐标分别是1,3,5,…,共2015个连续奇数,过点P1,P2,P3,…,P2015分别作y轴的平行线,与y=$\frac{3}{x}$的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…Q2015(x2015,y2015),则y2015=2014.5.
两个反比例函数y=$\frac{3}{x}$,y=$\frac{6}{x}$在第一象限内的图象如图所示,点P1,P2,P3,…,P2015在反比例函数y=$\frac{6}{x}$图象上,它们的横坐标分别是x1,x2,x3,…,x2015,纵坐标分别是1,3,5,…,共2015个连续奇数,过点P1,P2,P3,…,P2015分别作y轴的平行线,与y=$\frac{3}{x}$的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…Q2015(x2015,y2015),则y2015=2014.5. 已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC. 已知:如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
已知:如图,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.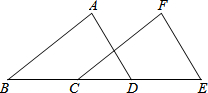 如图,点B、C、D、E在同一直线上,BC=DE,AB=FC,AD=EF.
如图,点B、C、D、E在同一直线上,BC=DE,AB=FC,AD=EF.
 如图,BD平分∠ABC,∠DBE=29°,且∠CBE比∠ABE的3倍还大18°,求∠CBD的度数.
如图,BD平分∠ABC,∠DBE=29°,且∠CBE比∠ABE的3倍还大18°,求∠CBD的度数.