题目内容
11．
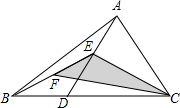如图，在△ABC中，点D是BC边上的任意一点，E是AD中点，F是BE中点，连结CE，CF，若点D从点B运动到点C，则△CEF的面积（ ）| A． | 一直变大 | B． | 一直变小 | C． | 先变大再变小 | D． | 不变 |
分析 根据三角形底边的中线把三角形的面积分为相等的两部分即可得出结论．
解答 解：∵点F是BE的中点，
∴S△CEF=$\frac{1}{2}$S△BCE；
∵E是AD中点，
∴S△BCE=$\frac{1}{2}$S△ABC，
∴S△CEF=$\frac{1}{4}$S△ABC，
∴△CEF的面积不变．
故选D．
点评 本题考查的是三角形的面积，熟知三角形底边的中线把三角形的面积分为相等的两部分是解答此题的关键．
练习册系列答案
相关题目
14．某单位为节省经费，在两个月内开支从每月2500元降到1600元，若平均每月降低开支的百分率为x，则下列方程符合题意的是（ ）
| A． | 2500（1-x）2=1600 | B． | 1600（1-x）2=2500 | C． | 2500（1+x）2=1600 | D． | 1600（1+x）2=2500 |
如图．在平面直角坐标系xOy中．点A的坐标为（-1，1），点B是x轴上的一动点．以AB为斜边作等腰直角△ABC，AM⊥x轴于M．当点C（x，y）在第一象限内时，下列图象中，可以表示y与x的函数关系的是（ ）
16．
如图，在△ABC中，D，E分别是AB，BC边上的点，且DE∥AC，若S△BDE：S△DEC=1：3，则S△BDE：S四边形ACED的值为（ ）
如图，在△ABC中，D，E分别是AB，BC边上的点，且DE∥AC，若S△BDE：S△DEC=1：3，则S△BDE：S四边形ACED的值为（ ）| A． | 1：9 | B． | 1：12 | C． | 1：15 | D． | 1：16 |
1．
如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）经过点A（1，0）和点B（0，-2），且顶点在第三象限，记m=a-b+c，则m的取值范围是（ ）
如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）经过点A（1，0）和点B（0，-2），且顶点在第三象限，记m=a-b+c，则m的取值范围是（ ）| A． | -1＜m＜0 | B． | -2＜m＜0 | C． | -4＜m＜-2 | D． | -4＜m＜0 |