题目内容
1. 如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)经过点A(1,0)和点B(0,-2),且顶点在第三象限,记m=a-b+c,则m的取值范围是( )
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)经过点A(1,0)和点B(0,-2),且顶点在第三象限,记m=a-b+c,则m的取值范围是( )| A. | -1<m<0 | B. | -2<m<0 | C. | -4<m<-2 | D. | -4<m<0 |
分析 求出a>0,b>0,把x=1代入求出a=2-b,b=2-a,把x=-1代入得出y=a-b+c=2a-4,求出2a-4的范围即可.
解答 解:∵二次函数的图象开口向上,
∴a>0,
∵对称轴在y轴的左边,
∴-$\frac{b}{2a}$<0,
∴b>0,
∵图象与y轴的交点坐标是(0,-2),过(1,0)点,
代入得:a+b-2=0,
∴a=2-b,b=2-a,
∴y=ax2+(2-a)x-2,
当x=-1时,y=a-b+c=a-(2-a)-2=2a-4,
∵b>0,
∴b=2-a>0,
∴a<2,
∵a>0,
∴0<a<2,
∴0<2a<4,
∴-4<2a-4<0,
∵y=a-b+c=a-(2-a)-2=2a-4,
∴-4<a-b+c<0,
即-4<m<0.
故选:D.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c).

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
11.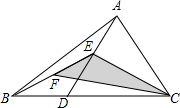 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )| A. | 一直变大 | B. | 一直变小 | C. | 先变大再变小 | D. | 不变 |
12.点A(-0.2,10)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.若直线y=2x-4与直线y=kx+6的交点在x轴上,则k的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |