题目内容
6. 如图.在平面直角坐标系xOy中.点A的坐标为(-1,1),点B是x轴上的一动点.以AB为斜边作等腰直角△ABC,AM⊥x轴于M.当点C(x,y)在第一象限内时,下列图象中,可以表示y与x的函数关系的是( )
如图.在平面直角坐标系xOy中.点A的坐标为(-1,1),点B是x轴上的一动点.以AB为斜边作等腰直角△ABC,AM⊥x轴于M.当点C(x,y)在第一象限内时,下列图象中,可以表示y与x的函数关系的是( )| A. |  | B. |  | C. |  | D. |  |
分析 过A作AD⊥y轴于D,过C作CF⊥y轴于F,由已知条件动点AM=OM=1,推出四边形AMOD是正方形,根据相似三角形的性质得到∠ADC=∠AOB=135°,推出△CDF是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.
解答  解:过A作AD⊥y轴于D,过C作CF⊥y轴于F,
解:过A作AD⊥y轴于D,过C作CF⊥y轴于F,
∵AM⊥x轴于M,点A的坐标为(-1,1),
∴AM=OM=1,
∴四边形AMOD是正方形,
∴OD=AD=1,∠AOD=∠OAD=45°,
∵△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CAD=∠OAB,
∵$\frac{AD}{AO}=\frac{AC}{AB}$=$\frac{\sqrt{2}}{2}$,
∴△ACD∽△ABO,
∴∠ADC=∠AOB=135°,
∴∠CDF=45°,
∴△CDF是等腰直角三角形,
∴DF=CF=x,
∵DF=y-1,
∴y-1=x,
∴y=x+1,
故选C.
点评 本题考查了动点问题的函数图象,相似三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
1.若$\sqrt{-(5-a)^{2}}$是一个实数,则满足这个条件的a有( )
| A. | 0个 | B. | 1个 | C. | 4个 | D. | 无数多个 |
11.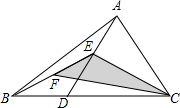 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )| A. | 一直变大 | B. | 一直变小 | C. | 先变大再变小 | D. | 不变 |
15.下列性质中正方形具有而矩形不一定具有的是( )
| A. | 四个角郡相等 | B. | 对边平行且相等 | C. | 对角线相等 | D. | 对角线互相垂直 |
 如图,直线y=kx+b与抛物线y=ax2相交于点A,B,与x轴相交于点C.
如图,直线y=kx+b与抛物线y=ax2相交于点A,B,与x轴相交于点C. 如图,以锐角△ABC的边AB为直径作⊙O,交AC、BC于E、D两点,DF⊥AB.若AC=14,CD=4,7sinC=3tanB,则BD=( )
如图,以锐角△ABC的边AB为直径作⊙O,交AC、BC于E、D两点,DF⊥AB.若AC=14,CD=4,7sinC=3tanB,则BD=( )