题目内容
3.已知方程组$\left\{\begin{array}{l}{3x+y=12}\\{4x+ay=2}\end{array}\right.$有负整数解(a为整数),求a的值.分析 先解方程组,用a表示出y,再根据方程组有负整数解,判断整数a的值即可.
解答 解:解方程组$\left\{\begin{array}{l}{3x+y=12}\\{4x+ay=2}\end{array}\right.$,消去x可得,y=$\frac{42}{4-3a}$
因为方程组有负整数解(a为整数),
所以4-3a=-1或-42或-2或-21或-3或-14或-6或-7.
所以a=$\frac{5}{3}$或$\frac{46}{3}$或2或$\frac{25}{3}$或$\frac{7}{3}$或6或$\frac{10}{3}$或$\frac{11}{3}$,
因为a为整数,
所以a=2或6,
当a=2时,y=-21,x=11(不合题意),
当a=6时,y=-3,x=5(不合题意),
所以当a为整数时,方程组$\left\{\begin{array}{l}{3x+y=12}\\{4x+ay=2}\end{array}\right.$无负整数解.
点评 本题主要考查了二元一次方程组的解法以及正整数解问题.当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
11.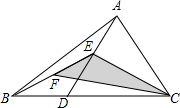 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
 如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )
如图,在△ABC中,点D是BC边上的任意一点,E是AD中点,F是BE中点,连结CE,CF,若点D从点B运动到点C,则△CEF的面积( )| A. | 一直变大 | B. | 一直变小 | C. | 先变大再变小 | D. | 不变 |
8. 二次函数y=ax2+bx+c的图象如图所示,P(n,2)是图象上的一点,且AP⊥BP,则a=( )
二次函数y=ax2+bx+c的图象如图所示,P(n,2)是图象上的一点,且AP⊥BP,则a=( )
 二次函数y=ax2+bx+c的图象如图所示,P(n,2)是图象上的一点,且AP⊥BP,则a=( )
二次函数y=ax2+bx+c的图象如图所示,P(n,2)是图象上的一点,且AP⊥BP,则a=( )| A. | -2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
15.下列性质中正方形具有而矩形不一定具有的是( )
| A. | 四个角郡相等 | B. | 对边平行且相等 | C. | 对角线相等 | D. | 对角线互相垂直 |
12.点A(-0.2,10)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,以锐角△ABC的边AB为直径作⊙O,交AC、BC于E、D两点,DF⊥AB.若AC=14,CD=4,7sinC=3tanB,则BD=( )
如图,以锐角△ABC的边AB为直径作⊙O,交AC、BC于E、D两点,DF⊥AB.若AC=14,CD=4,7sinC=3tanB,则BD=( )