题目内容
16．
如图，在△ABC中，D，E分别是AB，BC边上的点，且DE∥AC，若S△BDE：S△DEC=1：3，则S△BDE：S四边形ACED的值为（ ）| A． | 1：9 | B． | 1：12 | C． | 1：15 | D． | 1：16 |
分析 先由S△BDE：S△DEC=1：3得出BE：CE=1：3，故可得出BE：BC=1：4，再由DE∥AC可知△BDE∽△BAC，再由相似三角形的性质即可得出结论．
解答 解：∵S△BDE：S△DEC=1：3，
∴BE：CE=1：3，
∴BE：BC=1：4．
∵DE∥AC，
∴△BDE∽△BAC，
∴$\frac{{S}_{△BDE}}{{S}_{△BAC}}$=$\frac{1}{16}$，
∴S△BDE：S四边形ACED=1：15．
故选C．
点评 本题考查的是相似三角形的判定与性质，熟知相似三角形面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
19．在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
（1）请估计：当n很大时，摸到白球的概率约为0.6． （精确到0.1）
（2）估算盒子里有白球24个．
（3）若向盒子里再放入x个除颜色以外其它完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，那么可以推测出x最有可能是10．
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
| 摸到白球的频率 $\frac{m}{n}$ | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
（2）估算盒子里有白球24个．
（3）若向盒子里再放入x个除颜色以外其它完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，那么可以推测出x最有可能是10．
4．
如图，在△ABC中，∠ACB=90°，AC=BC，AD平分∠BAC，CE⊥AD交AB于点E，BE=CF，BF交CE于点P，连接PD，下列结论：①AC=AE；②CD=BE；③PB=PF；④DP⊥BF，其中正确的结论是（ ）
如图，在△ABC中，∠ACB=90°，AC=BC，AD平分∠BAC，CE⊥AD交AB于点E，BE=CF，BF交CE于点P，连接PD，下列结论：①AC=AE；②CD=BE；③PB=PF；④DP⊥BF，其中正确的结论是（ ）| A． | ①②③④ | B． | ①②③ | C． | ①② | D． | ①③ |
11．
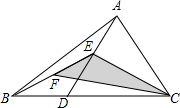如图，在△ABC中，点D是BC边上的任意一点，E是AD中点，F是BE中点，连结CE，CF，若点D从点B运动到点C，则△CEF的面积（ ）
如图，在△ABC中，点D是BC边上的任意一点，E是AD中点，F是BE中点，连结CE，CF，若点D从点B运动到点C，则△CEF的面积（ ）| A． | 一直变大 | B． | 一直变小 | C． | 先变大再变小 | D． | 不变 |
1．等边三角形的面积为8$\sqrt{3}$cm2，则它的高为（ ）
| A． | 2$\sqrt{2}$cm | B． | 4$\sqrt{2}$cm | C． | 2$\sqrt{6}$cm | D． | 2$\sqrt{5}$cm |
8．
二次函数y=ax2+bx+c的图象如图所示，P（n，2）是图象上的一点，且AP⊥BP，则a=（ ）
二次函数y=ax2+bx+c的图象如图所示，P（n，2）是图象上的一点，且AP⊥BP，则a=（ ）| A． | -2 | B． | -3 | C． | -$\frac{1}{2}$ | D． | -$\frac{1}{3}$ |
5．已知$\left\{\begin{array}{l}{2a+b=3}\\{3a-4b=10}\end{array}\right.$，则a-b等于（ ）
| A． | 3 | B． | $\frac{3}{4}$ | C． | 4 | D． | 1 |