题目内容
2.如图1,在菱形ABCD中,∠A=60°.点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.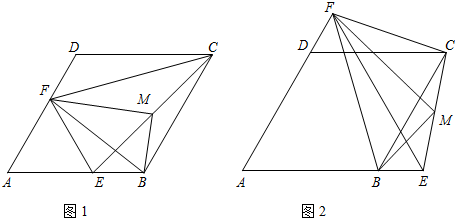
(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证:BM⊥FM;
(3)如图2,若点E,F分别是边AB,AD延长线上的点,其它条件不变,结论BM⊥FM是否仍然成立(不需证明).
分析 (1)根据已知和菱形的性质证明△CBE≌△CDF,得到BE=DF,证明△AEF是等边三角形,求出EF的长;
(2)延长BM交DC于点N,连结FN,证明△CMN≌△EMB,得到NM=MB,证明△FDN≌△BEF,得到FN=FB,得到BM⊥MF;
(3)延长BM交DC的延长线于点N,连结FN,与(2)的证明方法相似证明BM⊥MF.
解答 (1)解:∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠D=∠CBE,
又∵∠BCE=∠DCF,
∴△CBE≌△CDF,
∴BE=DF.
又∵AB=AD,∴AB-BE=AD-DF,即AE=AF,
又∵∠A=60°,∴△AEF是等边三角形,
∴EF=AF,
∵AF=1,∴EF=1.
(2)证明:如图1,延长BM交DC于点N,连结FN,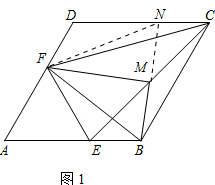
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,∴∠A+∠D=180°,
又∵∠A=60°,∴∠D=120°,
∴∠D=∠BEF.
又∵DN=EF,BE=DF.
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,∴BM⊥MF;
(3)结论BM⊥MF仍然成立.
证明:如图2,延长BM交DC的延长线于点N,连结FN,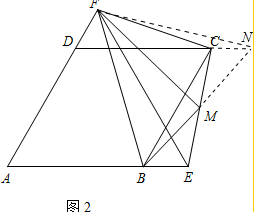
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,∴∠A+∠FDC=180°,
又∵∠A=60°,∴∠FDC=120°,
∴∠FDC=∠BEF.
又∵DN=EF,BE=DF.
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,
∴BM⊥MF.
点评 本题考查的是菱形的性质、全等三角形的判定和性质以及等腰三角形的性质,正确作出辅助线、构造全等三角形是解题的关键.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案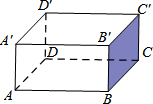 如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )
如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C′处,若长方体的长AB=4cm,宽BC=3cm,高BB′=2cm,则蚂蚁爬行的最短路径是( )| A. | $\sqrt{53}$cm | B. | $\sqrt{45}$cm | C. | $\sqrt{41}$cm | D. | 7cm |
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
| A. | 12 | B. | 24 | C. | 40 | D. | 48 |
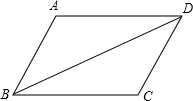 在平行四边形ABCD中,∠BAD=110°,∠ABD=30°,则∠CBD度数为( )
在平行四边形ABCD中,∠BAD=110°,∠ABD=30°,则∠CBD度数为( )| A. | 30° | B. | 40° | C. | 70° | D. | 50° |

各年级学生人数统计表
| 年级 | 七年级 | 八年级 | 九年级 |
| 学生人数 | 180 | 165 | 160 |
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校九年级学生比八年级学生少5人,请你补全上表,并利用样本数据估计全校三个年级学生中最喜欢跳绳运动的人数约为多少?