题目内容
7.如图1,在平面直角坐标系中,二次函数y=$\frac{1}{4}$x2+bx的图象与x轴交于点A(6,0),△OBC的B点坐标(3,4),C点坐标为(5,0).(1)求二次函数的关系式;
(2)将△OBC沿边BC翻折,点O落在点D,请求出点D的坐标并判断点D是否在二次函数的图象上;
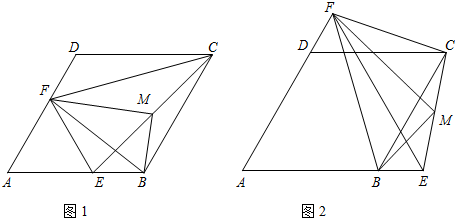
(3)在(2)的条件下,如图2,点E的坐标为(0,8),有一动点P从E点出发沿EO方向以2个单位/s的速度向下运动,过点P的直线l平行于x轴,当点P运动到点O时停止运动,设运动时间为t(s),其中0≤t≤4.请探究直线l上是否存在点H,使得△ODH为直角三角形?若存在,请直接写出满足条件的点H的个数及相应t的取值范围,不需说明理由;若不存在,请说明理由.

分析 (1)把A点坐标代入y=$\frac{1}{4}$x2+bx,求出b的值,即可求出二次函数的关系式.
(2)首先由B、C坐标证得OB=OC,再根据翻折的性质可证得四边形OBDC为菱形,进而判断出四边形BMND是矩形,所以MN=BD=5,DN=BM=4,ON=OM+MN=3+5=8,据此求出点D的坐标,然后把点D的坐标代入抛物线解析式,即可判断出点D是否在二次函数的图象上.
(3)首先求出当l和BD重合时,l和x轴重合时,t的值各是多少;然后分类讨论:①当0≤t<3-$\sqrt{5}$,t=2或t=4时;②当t=3-$\sqrt{5}$时;③当3-$\sqrt{5}$<t<2,或2<t<4时;根据△ODH为直角三角形,写出所有满足条件的点H的个数及相应t的取值范围即可.
解答 解:(1)将点A(6,0)代入y=$\frac{1}{4}$x2+bx,可得
0=$\frac{1}{4}{×6}^{2}$+6b,
解得b=-$\frac{3}{2}$,
∴二次函数的关系式是y=$\frac{1}{4}$x2-$\frac{3}{2}$x.
(2)如图1,过点B作BM⊥x轴于点M,过点D作DN⊥x轴于点N,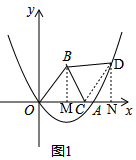 ,
,
将△OBC沿边BC翻折,点O落在点D,
∵△OBC的B点坐标(3,4),C点坐标为(5,0),
∴OM=3,BM=4,OC=5,
∴OB=$\sqrt{{OM}^{2}{+BM}^{2}}=\sqrt{{3}^{2}{+4}^{2}}=5$,
∴OB=OC,
∵将△OBC沿边BC翻折得到△DBC,
∴△OBC≌△DBC,
∴OB=DB,OC=DC,
又∵OB=OC,
∴OB=DB=OC=DC,
∴四边形OBDC是菱形,
∴BD∥x轴,
∵BM⊥x轴,DN⊥x轴,
∴BM∥DN,
∴四边形BMND是平行四边形,
∵∠BMN=90°,
∴四边形BMND是矩形,
∴MN=BD=5,DN=BM=4,
∴ON=OM+MN=3+5=8,
∴点D的坐标是(8,4),
∵当x=8时,y=$\frac{1}{4}$×82-$\frac{3}{2}$×8=4,
∴点D是否在二次函数的图象上.
(3)由(2)可得四边形OBDC是菱形,
∴BD∥x轴,
当l和BD重合时,
∵8-2t=4,
∴t=2,点H的个数是2个;
当l和x轴重合时,
∵8-2t=0,
∴t=4,点H的个数是2个;
①当0≤t<3-$\sqrt{5}$,t=2或t=4时,
点H的个数是2个.
②当t=3-$\sqrt{5}$时,
点H的个数是3个.
③当3-$\sqrt{5}$<t<2,或2<t<4时,
点H的个数是4个.
点评 (1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了待定系数法求二次函数解析式问题的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,要熟练掌握.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | $\sqrt{{{0.5}^2}}$=0.5 | B. | $\sqrt{\frac{4}{3}}=\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{8}×\sqrt{\frac{1}{2}}=2$ | D. | ${(-7\sqrt{\frac{2}{7}})^2}=7\frac{2}{7}$ |
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 同位角相等 | |
| C. | 垂直于同一条直线的两条直线互相平行 | |
| D. | 对顶角相等 |
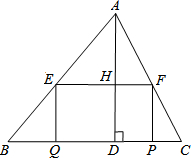 如图,在△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H,设ED=x.
如图,在△ABC中,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H,设ED=x.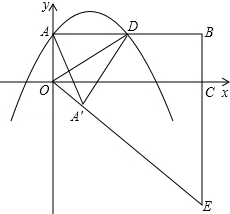 如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,D为边AB的中点,一抛物线y=-x2+2mx+m(m>0)经过点A、D
如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,D为边AB的中点,一抛物线y=-x2+2mx+m(m>0)经过点A、D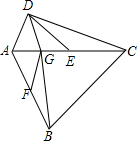 如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,
如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,