题目内容
17.求证:关于x的一元二次方程x2-3(m-1)x+$\frac{5}{2}$m2-4m+3=0没有实数根.分析 要证明方程没有实数根,那么只要证明△<0即可.
解答 证明:△=9(m-1)2-4($\frac{5}{2}$m2-4m+3)
=9m2-18m+9-10m2+16m-12
=-m2-2m-3
=-(m+1)2-2,
∵-(m+1)2≤0,
∴-(m+1)2-2<0,
∴该方程没有实数根.
点评 本题主要考查根的判别式,熟练掌握一元二次方程的根的情况与判别式△的符号的关系是关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12. 如图所示的是一次函数y=kx+b(k≠0)的图象,则关于x的不等式k(x-1)+b>0的解集为( )
如图所示的是一次函数y=kx+b(k≠0)的图象,则关于x的不等式k(x-1)+b>0的解集为( )
 如图所示的是一次函数y=kx+b(k≠0)的图象,则关于x的不等式k(x-1)+b>0的解集为( )
如图所示的是一次函数y=kx+b(k≠0)的图象,则关于x的不等式k(x-1)+b>0的解集为( )| A. | x<3 | B. | x>3 | C. | x<4 | D. | x>4 |
13.若单项式-2x5yzn+1和$\frac{1}{3}$x2m+1yz3是同类项,则m,n的值分别为( )
| A. | 1,2 | B. | 2,2 | C. | 3,3 | D. | 2,1 |
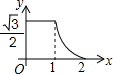
 如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )


 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,O为BC的中点,OE平分∠AOB,与AB相交于点E,OD平分∠AOC,与AC相交于点D.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,O为BC的中点,OE平分∠AOB,与AB相交于点E,OD平分∠AOC,与AC相交于点D.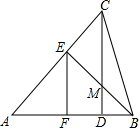 在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.
在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.