题目内容
12. 如图所示的是一次函数y=kx+b(k≠0)的图象,则关于x的不等式k(x-1)+b>0的解集为( )
如图所示的是一次函数y=kx+b(k≠0)的图象,则关于x的不等式k(x-1)+b>0的解集为( )| A. | x<3 | B. | x>3 | C. | x<4 | D. | x>4 |
分析 把(3,0),(0,2)代入y=kx+b求得k和b的值,则不等式化为-$\frac{2}{3}$(x-1)+2>0,解不等式即可.
解答 解:把(3,0),(0,2)代入y=kx+b得$\left\{\begin{array}{l}{3k+b=0}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=2}\end{array}\right.$,
所以k(x-1)+b>0化为-$\frac{2}{3}$(x-1)+2>0,
解得x<4,
故选C.
点评 本题考查了一次函数与一元一次不等式,根据待定系数法求得k和b的值是解题的关键.

练习册系列答案
相关题目
3.一次函数y=2x-4的图象在第一象限,则x的取值范围是( )
| A. | x<0 | B. | x>0 | C. | x>2 | D. | x<2 |
7.下列图形中,不是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 菱形 | D. | 矩形 |
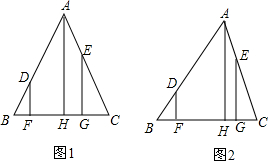 已知△ABC,点D,E分别在边AB,AC上,分别过A,D,E作BC的垂线,垂足为H,F,G.
已知△ABC,点D,E分别在边AB,AC上,分别过A,D,E作BC的垂线,垂足为H,F,G.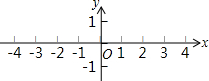 如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.
如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.