题目内容
7.在平面直角坐标系中,已知A(1,4)、B(3,1),P是坐标轴上一点,当P的坐标为多少时,AP+BP取最小值,最小值为多少?当P的坐标为多少时,AP-BP取最大值,最大值为多少?分析 如图1,作点A关于y轴的对称点A′,连接A′B交y轴于点P,求得直线A′B的解析式为y=-$\frac{3}{4}$x+$\frac{13}{4}$,当x=0时,y=$\frac{13}{4}$,得到P(0,$\frac{13}{4}$),根据勾股定理得到A′B=$\sqrt{{3}^{2}+{4}^{2}}$=5,如图2,作点A关于x轴的对称点A′,连接A′B交y轴于点P,求得直线A′B的解析式为y=$\frac{5}{2}$x-$\frac{13}{2}$,当y=0时,x=$\frac{13}{5}$,得到P($\frac{13}{5}$,0);根据勾股定理得到A′B=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$,即可得到结论,如图3,连接AB并延长交x轴于P,则PA-PB的值最大,求得直线AB的解析式为y=-$\frac{3}{2}$x+$\frac{11}{2}$,当y=0时,x=$\frac{11}{3}$,得到P($\frac{11}{3}$,0),根据勾股定理得到PA-PB=AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,即可得到结论.
解答 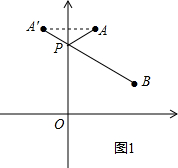 解:如图1,作点A关于y轴的对称点A′,连接A′B交y轴于点P,
解:如图1,作点A关于y轴的对称点A′,连接A′B交y轴于点P,
∵A(1,4),
∴A′(-1,4),
设直线A′B的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{3k+b=1}\\{-k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{13}{4}}\end{array}\right.$,
∴直线A′B的解析式为y=-$\frac{3}{4}$x+$\frac{13}{4}$,
当x=0时,y=$\frac{13}{4}$,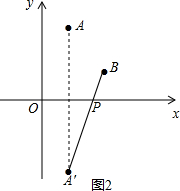
∴P(0,$\frac{13}{4}$),
∴A′B=$\sqrt{{3}^{2}+{4}^{2}}$=5,
如图2,作点A关于x轴的对称点A′,连接A′B交y轴于点P,
∵A(1,4),
∴A′(1,-4),
设直线A′B的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{3k+b=1}\\{k+b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{5}{2}}\\{b=-\frac{13}{2}}\end{array}\right.$,
∴直线A′B的解析式为y=$\frac{5}{2}$x-$\frac{13}{2}$,
当y=0时,x=$\frac{13}{5}$,
∴P($\frac{13}{5}$,0);
∴A′B=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$,
∵5<$\sqrt{29}$,
∴当P的坐标为(0,$\frac{13}{4}$)时,AP+BP取最小值,最小值为5;
如图3,∵4>1,
∴P在x轴上,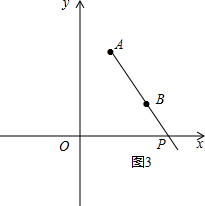 连接AB并延长交x轴于P,
连接AB并延长交x轴于P,
则PA-PB的值最大,
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{4=k+b}\\{1=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{11}{2}}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{3}{2}$x+$\frac{11}{2}$,
当y=0时,x=$\frac{11}{3}$,
∴P($\frac{11}{3}$,0),
PA-PB=AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴当P的坐标为($\frac{11}{3}$,0)时,AP-BP取最大值,最大值为$\sqrt{13}$.
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 0.118×107 | B. | 1.18×106 | C. | 11.8×106 | D. | 1.18×107 |
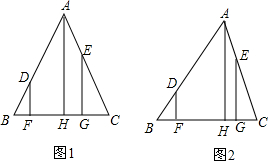 已知△ABC,点D,E分别在边AB,AC上,分别过A,D,E作BC的垂线,垂足为H,F,G.
已知△ABC,点D,E分别在边AB,AC上,分别过A,D,E作BC的垂线,垂足为H,F,G.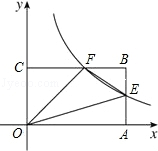 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则: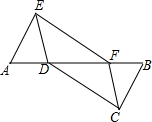 如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.
如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.