题目内容
8. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )| A. |  | B. |  | C. |  | D. | 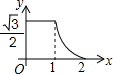 |
分析 根据题意可知在点C′移动到点C的过程中,重合部分的面积不变,可以算出相应的面积,C′继续向右移动可以求出相应的重合部分的面积,从而可得到相应的函数解析式,从个可以明确哪个选项是正确的.
解答 解:由题意可知,
当C′从左向右移动到C的位置时,△ABC与△A′B′C′重合的面积是△A′B′C′的面积,
∵△A′B′C′是等边三角形,边长等于1,
∴${S}_{△A′B′C′}=\frac{1×1×sin60°}{2}=\frac{\frac{\sqrt{3}}{2}}{2}=\frac{\sqrt{3}}{4}$;
当点C′继续从C向右移动时的重合部分的面积是:$\frac{[1-(x-1)][1-(x-1)]×sin60°}{2}$=$\frac{\sqrt{3}}{4}(2-x)^{2}$,此时函数图象为抛物线,开口向上,顶点坐标是(2,0),
故选B.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,知道各段对应的重合部分的面积如何变化,可以求出相应的重合部分的面积,与函数结合在一起,利用数形结合的思想解答问题.

练习册系列答案
相关题目
3.一次函数y=2x-4的图象在第一象限,则x的取值范围是( )
| A. | x<0 | B. | x>0 | C. | x>2 | D. | x<2 |
13.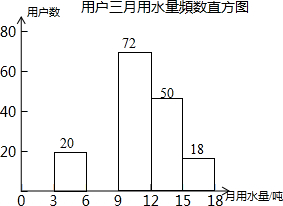 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=40,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.请估计该社区约有多少户家庭三月份的用水量超过基本月用水量?
 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用水量h(吨) | 频数 | 频率 |
| h≤3 | 0 | 0 |
| 3<h≤6 | 20 | 0.10 |
| 6<h≤9 | m | 0.20 |
| 9<h≤12 | 72 | 0.36 |
| 12<h≤15 | 50 | n |
| 15<h≤18 | 18 | 0.09 |
| 18<h | 0 | 0 |
(1)在频数分布表中:m=40,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.请估计该社区约有多少户家庭三月份的用水量超过基本月用水量?
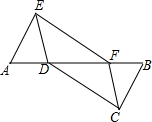 如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.
如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.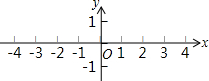 如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.
如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.