题目内容
9.观察下面式子的化简过程:$\frac{2\sqrt{6}}{\sqrt{2}+\sqrt{3}+\sqrt{5}}$=$\frac{(2+2\sqrt{6}+3)-5}{\sqrt{2}+\sqrt{3}+\sqrt{5}}$=$\frac{(\sqrt{2}+\sqrt{3})^{2}-(\sqrt{5})^{2}}{\sqrt{2}+\sqrt{3}+\sqrt{5}}$=$\sqrt{2}$+$\sqrt{3}$-$\sqrt{5}$.
化简$\frac{4\sqrt{10}}{\sqrt{5}+\sqrt{13}+\sqrt{8}}$,并将这一问题作尽可能的推广.
分析 根据题意把原式的分子化为平方差的形式,再约分即可.
解答 解:原式=$\frac{2\sqrt{40}}{\sqrt{5}+\sqrt{13}+\sqrt{8}}$
=$\frac{(5+2\sqrt{40}+8)-13}{\sqrt{5}+\sqrt{13}+\sqrt{8}}$
=$\frac{{(\sqrt{5}+\sqrt{8})}^{2}-(\sqrt{13})^{2}}{\sqrt{5}+\sqrt{13}+\sqrt{8}}$
=$\sqrt{5}$+$\sqrt{8}$-$\sqrt{13}$.
点评 本题考查的是分母有理化,根据题意找出有理化因式是解答此题的关键.

练习册系列答案
相关题目
18.如果半径分别为2和3的两圆外切,那么这两个圆的圆心距是( )
| A. | 1 | B. | 5 | C. | 1或5 | D. | 大于1且小于5 |
 已知在△ABC中,AC⊥BC,AC=BC,CF=CD,求证:BF=AD,BF⊥AD.
已知在△ABC中,AC⊥BC,AC=BC,CF=CD,求证:BF=AD,BF⊥AD.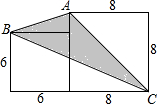 如图,求阴影部分的面积.
如图,求阴影部分的面积.