题目内容
14. 已知在△ABC中,AC⊥BC,AC=BC,CF=CD,求证:BF=AD,BF⊥AD.
已知在△ABC中,AC⊥BC,AC=BC,CF=CD,求证:BF=AD,BF⊥AD.
分析 先证出∠CBF=∠CAD,再由ASA证明△BCF≌△ACD,得出对应边相等即可;根据HL证Rt△BCF≌Rt△ADC,推出∠FBC=∠DAC,根据∠BCF=90°求出∠CBF+∠BFC=90°,推出∠DAC+∠AFE=90°,求出∠AEF=90°即可.
解答 证明:∵AC⊥BD,BE⊥AD,
∴∠BCF=∠ACD=∠BED=90°,
∴∠CBF+∠D=90°,∠CAD+∠D=90°,
∴∠CBF=∠CAD,
在△BCF和△ACD中,
$\left\{\begin{array}{l}{∠BCF=∠ACD}\\{BC=AC}\\{∠CBF=∠CAD}\end{array}\right.$,
∴△BCF≌△ACD(ASA),
∴BF=AD;
∵AC⊥BD,
∴∠BCF=∠ACD=90°,
在Rt△BCF和Rt△ACD中,
$\left\{\begin{array}{l}{BF=AD}\\{CF=CD}\end{array}\right.$,
∴Rt△BCF≌Rt△ACD(HL),
∴∠FBC=∠CAD,
∵∠BCF=90°,
∴∠CBF+∠BFC=90°,
∵∠BFC=∠AFE,
∴∠CAD+∠AFE=90°,
∴∠AEF=180°-90°=90°,
∴AD⊥BF.
点评 本题考查了全等三角形的性质和判定,三角形内角和定理的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.△ABC中,∠A=30°,∠B=45°,若AC=8,则BC2的值是( )
| A. | 48 | B. | 96 | C. | 16 | D. | 32 |
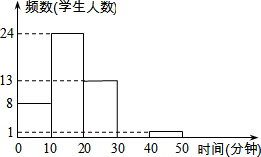 李老师为了解班里学生的作息时间,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:
李老师为了解班里学生的作息时间,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题: