题目内容
3.某园林里有两棵相距8米的树,一棵高8米,另一棵高2米.若有一只鸟从一棵树的顶端飞到另一棵树的顶端,则小鸟至少要飞10米.分析 根据题意画出图形,再利用勾股定理求解即可.
解答  解:如图,过点A作AE⊥CD于点E,
解:如图,过点A作AE⊥CD于点E,
∵AB⊥BD,CD⊥BD,AE⊥CD,
∴四边形ABDE是矩形.
∵AB=2米,CD=BD=8米,
∴AE=BD=8米,CE=8-2=6米,
∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10(米).
故答案为:10.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
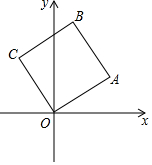 已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).
已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$). 如图,一透明的圆柱体玻璃杯,从内部测得底部直径为6cm,杯深8cm.今有一根长为16cm的吸管如图放入杯中,露在杯口外的长度为h,则h的变化范围是:6cm≤h≤8cm.
如图,一透明的圆柱体玻璃杯,从内部测得底部直径为6cm,杯深8cm.今有一根长为16cm的吸管如图放入杯中,露在杯口外的长度为h,则h的变化范围是:6cm≤h≤8cm.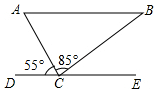 如图,在△ABC中,∠ACB=85°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是40°.
如图,在△ABC中,∠ACB=85°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是40°.