题目内容
计算:(24+22+1)×(44+42+1)×(64+62+1)×(84+82+1)×(104+102+1)÷((34+32+1)×(54+52+1)×(74+72+1)×(94+92+1)×(114+112+1)).
考点:有理数无理数的概念与运算
专题:
分析:利用(x4+x2+1)=(x2+x+1)(x2-x+1);x2-x+1=(x-1)2+(x-1)+1,进而将原式变形,进而化简求值即可.
解答:解:∵(x4+x2+1)=(x2+x+1)(x2-x+1);x2-x+1=(x-1)2+(x-1)+1;
∴原式=
=
=
=
.
∴原式=
| (22+2+1)(22-2+1)(42+4+1)(42-4+1)(62+6+1)(62-6+1)(82+8+1)(82-8+1)(102+10+1)(102-10+1) |
| (32+3+1)(32-3+1)(52+5+1)(52-5+1)(72+7+1)(72-7+1)(92+9+1)(92-9+1)(112+11+1)(112-11+1) |
=
| (22+2+1)(22-2+1)(42+4+1)(32+3+1)(62+6+1)(52+5+1)(82+8+1)(72+7+1)(102+10+1)(92+9+1) |
| (32+3+1)(22+2+1)(52+5+1)(42+4+1)(72+7+1)(62+6+1)(92+9+1)(82+8+1)(112+11+1)(102+10+1) |
=
| 22-2+1 |
| 112+11+1 |
=
| 3 |
| 133 |
点评:此题主要考查了有理数无理数的概念与运算,正确化简各式是解题关键.

练习册系列答案
相关题目
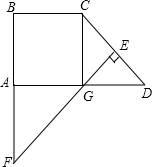 如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长.
如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长. 如图,四边形ABCD中,∠BAD与∠ADC的平分线AE、DE相交于点E,∠ABC与∠BCD的平分线BF、CF相交于点F,求∠E+∠F的度数.
如图,四边形ABCD中,∠BAD与∠ADC的平分线AE、DE相交于点E,∠ABC与∠BCD的平分线BF、CF相交于点F,求∠E+∠F的度数.