题目内容
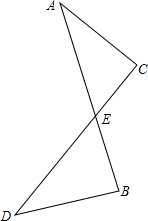 如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长.
如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长.考点:平行四边形的判定与性质,勾股定理
专题:
分析:过A作AF∥CD,过D作DF∥AC,两线交于F,连接BF,求出四边形AFDC是平行四边形,推出AF=CD,求出三角形FDB是直角三角形,根据勾股定理求出BF,求出三角形ABF是直角三角形,求出AF即可.
解答:解: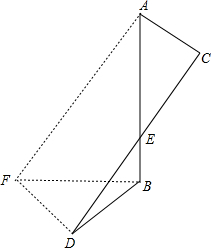
过A作AF∥CD,过D作DF∥AC,两线交于F,连接BF,
则四边形AFDC是平行四边形,
所以∠FAE=∠AEC=45°,∠C=∠AFD,AC=DF=3,
∵∠ABD+∠C=225°,
∴∠ABD+∠DFA=225°,
∴∠FDB=360°-225°-45°=90°,
∴△FDB是直角三角形,
∵DF=3,BD=4,
∴由勾股定理得:FB=5,
∴AB=FB,
∴∠BAF=∠AFB=45°,
∴∠ABF=90°,
∴由勾股定理得:AF=5
,
∵四边形AFDC是平行四边形,
∴CD=AF=5
.

过A作AF∥CD,过D作DF∥AC,两线交于F,连接BF,
则四边形AFDC是平行四边形,
所以∠FAE=∠AEC=45°,∠C=∠AFD,AC=DF=3,
∵∠ABD+∠C=225°,
∴∠ABD+∠DFA=225°,
∴∠FDB=360°-225°-45°=90°,
∴△FDB是直角三角形,
∵DF=3,BD=4,
∴由勾股定理得:FB=5,
∴AB=FB,
∴∠BAF=∠AFB=45°,
∴∠ABF=90°,
∴由勾股定理得:AF=5
| 2 |
∵四边形AFDC是平行四边形,
∴CD=AF=5
| 2 |
点评:本题考查了勾股定理,平行四边形的性质和判定,四边形的内角和定理的应用,题目比较典型,综合性比较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:在直角坐标系中,点A(-1,0),点B(3,0),点C在函数y=
已知:在直角坐标系中,点A(-1,0),点B(3,0),点C在函数y=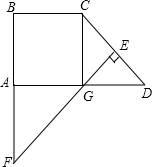 如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长.
如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长.