题目内容
7．
如图已知BE、EC分别平分∠ABC、∠BCD，且∠1与∠2互余，试说明AB∥DC．
分析 先用角平分线的性质得到∠ABC=2∠1，∠BCD=2∠2，再用∠1与∠2互余即可．
解答 解：∵∠1与∠2互余，
∴∠1+∠2=90°，
∵BE、EC分别平分∠ABC、∠BCD，
∴∠ABC=2∠1，∠BCD=2∠2，
∴∠ABC+∠BCD=2∠1+2∠2=2（∠1+∠2）=180°，
∴AB∥DC．
点评 此题是平行线的判定，还用到角平分线的意义，解本题的关键是用角平分线的意义得到∠ABC=2∠1，∠BCD=2∠2．
练习册系列答案
相关题目
10．下列图案中，既是中心对称图形也是轴对称图形的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
菱形ABCD中，∠B=60°，延长BC至E，使得CE=BC，点F在DE上，DF=6，AG平分∠BAF，与线段BC相交于点G，若CG=2，则线段AB的长度为10．
15．无论x取任何实数，代数式$\sqrt{{x}^{2}-6x+m}$都有意义，则m的取值范围是（ ）
| A． | m≥6 | B． | m≥8 | C． | m≥9 | D． | m≥12 |
2．
如图，在一块宽为20m，长为32m的矩形空地上，修筑宽相等的两条小路，两条路分别与矩形的边平行，如图，若使剩余（阴影）部分的面积为560m2，问小路的宽应是多少？设小路的宽为xcm，根据题意得（ ）
如图，在一块宽为20m，长为32m的矩形空地上，修筑宽相等的两条小路，两条路分别与矩形的边平行，如图，若使剩余（阴影）部分的面积为560m2，问小路的宽应是多少？设小路的宽为xcm，根据题意得（ ）| A． | 32x+20x=20×32-560 | B． | 32×20-20x×32x=560 | ||
| C． | （32-x）（20-x）=560 | D． | 以上都不正确 |
如图，菱形ABCD在平面直角坐标系中，点A位坐标原点，点B在x轴正半轴上，若点D的坐标为（1，$\sqrt{3}$），则点C的坐标为（3，$\sqrt{3}$）．
16．能使$\sqrt{x（x-6）}$=$\sqrt{x}$•$\sqrt{x-6}$成立的x的取值范围是（ ）
| A． | x≥6 | B． | x≥0 | C． | 0≤x≤6 | D． | x为一切实数 |
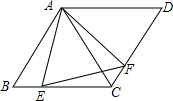如图，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为等边三角形，点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合．