题目内容
12．用配方法解方程x2-4x-5=0时，原方程应变形为（ ）| A． | （x-2）2=1 | B． | （x-2）2=9 | C． | （x-4）2=21 | D． | （x-4）2=11 |
分析 方程常数项移到右边，两边加上一次项系数一半的平方，利用完全平方公式变形即可得到结果．
解答 解：方程整理得：x2-4x=5，
配方得：x2-4x+4=9，即（x-2）2=9．
故选B．
点评 此题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
如图，M、P分别为△ABC的AB、AC上的点，且AM=BM，AP=2CP，BP与CM相交于N，已知PN=1，则PB的长为（ ）
3．
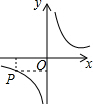如图，双曲线上任意点P，向x、y轴分别作垂线围成的矩形面积为2，那么反比例函数的解析式是（ ）
如图，双曲线上任意点P，向x、y轴分别作垂线围成的矩形面积为2，那么反比例函数的解析式是（ ）| A． | y=$\frac{1}{x}$ | B． | y=$\frac{2}{x}$ | C． | y=-$\frac{1}{x}$ | D． | y=-$\frac{2}{x}$ |
20．
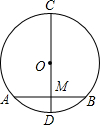如图，⊙O中，直径CD=10cm，弦AB⊥CD于点M，OM：MD=3：2，则AB的长是（ ）
如图，⊙O中，直径CD=10cm，弦AB⊥CD于点M，OM：MD=3：2，则AB的长是（ ）| A． | 4cm | B． | 5cm | C． | 6cm | D． | 8cm |
7．
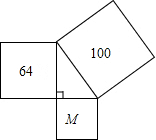如图，三个正方形围成一个直角三角形，64、100分别为所在正方形的面积，则图中字母所代表的正方形的边长是（ ）
如图，三个正方形围成一个直角三角形，64、100分别为所在正方形的面积，则图中字母所代表的正方形的边长是（ ）| A． | 36 | B． | $4\sqrt{41}$ | C． | 6 | D． | 164 |
如图，在?ABCD中，对角线AC⊥AB，O为AC的中点，经过点O的直线交AD于E，交BC于F，连结AF、CE，现在添加一个适当的条件，使四边形AFCE是菱形，下列条件：①OE=OA；②EF⊥AC；③AF平分∠BAC；④E为AD中点．正确的有（ ）个．
1．
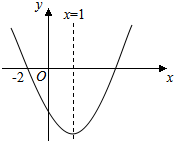二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：
①2a+b=0；
②a+c＞b；
③抛物线与x轴的另一个交点为（3，0）；
④abc＞0．
其中正确的结论的个数是（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b=0；
②a+c＞b；
③抛物线与x轴的另一个交点为（3，0）；
④abc＞0．
其中正确的结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．已知二次函数y=a（x-1）2+b（a≠0）有最大值2，则a、b的大小比较为（ ）
| A． | a＞b | B． | a＜b | C． | a=b | D． | 不能确定 |