题目内容
7．
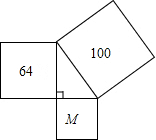如图，三个正方形围成一个直角三角形，64、100分别为所在正方形的面积，则图中字母所代表的正方形的边长是（ ）| A． | 36 | B． | $4\sqrt{41}$ | C． | 6 | D． | 164 |
分析 根据题意得出∠BCD=90°，BD2=100，BC2=81，由勾股定理求出CD2，得出CD即可．
解答 
解：如图所示：
根据题意得：∠BCD=90°，BD2=100，BC2=64，
∴CD2=BD2-BC2=36，
∴图中字母M所代表的正方形面积=BC2=36，
∴BC=$\sqrt{36}$=6．
故选：C．
点评 本题考查了正方形的性质、勾股定理、正方形面积的计算；熟练掌握正方形的性质和勾股定理是解决问题的关键．
练习册系列答案
百年学典课时学练测系列答案
相关题目
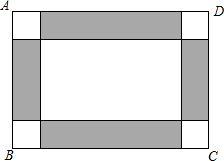暑假期间，某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面．已知这个矩形操场地面的长为100m，宽为80m，图案设计如图所示：操场的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都为小正方形的边长，在实际铺设的过程总，阴影部分铺红色地面砖，其余部分铺灰色地面砖．
12．用配方法解方程x2-4x-5=0时，原方程应变形为（ ）
| A． | （x-2）2=1 | B． | （x-2）2=9 | C． | （x-4）2=21 | D． | （x-4）2=11 |
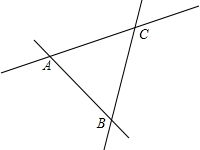如图所示，三条公路分别相交于A、B、C三点，现计划修建一个加油站，要求该加油站到三条公路的距离相等，用直尺和圆规作出加油站O的位置．（不写作法，请保留作图痕迹）
如图，已知抛物线y=ax2+bx+3与x轴交于点A（-3，0），B（1，0），P是其对称轴上的一个动点，连接PB、PC，下列结论：①2a+b＞-$\frac{3}{2}$；②对称轴是直线x=-1；③当y=3时，x=0；④PB+PC的最小值是3$\sqrt{2}$．其中正确的有（ ）