题目内容
5.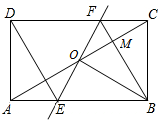 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E,点F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论错误的是( )| A. | FB⊥OC,OM=CM | B. | △EOB≌△CMB | ||
| C. | 四边形EBFD是菱形 | D. | MB:OE=3:2 |
分析 先证明△BOC是等边三角形,得FO=FC,BO=BC,故A正确,再证明四边形EBFD是平行四边形,由BE=BF推出四边形EBFD是菱形故C正确,设FM=a,则OF=OE=2a,FB=4a,由此推出D正确,由此不难得到答案.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AO=OC,
∴BO=OC=OA,
∵∠COB=60°,
∴△BCO是等边三角形,
∴∠ACB=∠OBC=60°,BC=OB,
∵FO=FC,BO=BC,
∴FB⊥OC,OM=CM,故A正确,
∴∠CBM=∠MBO=∠OBA=30°,∠FCO=∠FOC=30°,∠OFB=∠BFC=60°,
∴∠EBF=∠BFE=60°,
∴△EFB是等边三角形,
∴BE=BF,
在△FOC和△EOA中,
$\left\{\begin{array}{l}{∠FOC=∠AOE}\\{∠FCO=∠OAE}\\{OC=OA}\end{array}\right.$,
∴△FOC≌△EOA,
∴AE=CF,OE=OF,
∵DC=AB,
∴DF=EB,
∵DF∥EB,
∴四边形EBFD是平行四边形,
∵BE=BF,
∴四边形EBFD是菱形,故C正确,
设FM=a,
在RT△OFM中,∵∠FOM=30°,
∴OF=2FM=2a,
在RT△FOB中,∵∠FOB=90°,∠FBO=30°,
∴BF=2OF=4a,
∴BM=3a,
∴BM:OE=3:2,故D正确.
故选B.
点评 本题考查矩形的性质、等边三角形的判定和性质.全等三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.关于x的不等式(a-1)x<a+6的解集与不等式2x<4的解集相同,那么a的值为( )
| A. | 5 | B. | 8 | C. | -8 | D. | 9 |
16.下列两个三角形中,一定全等的是( )
| A. | 有一个角是40°,腰相等的两个等腰三角形 | |
| B. | 有一个角是100°,底相等的两个等腰三角形 | |
| C. | 两个等边三角形 | |
| D. | 有一条边相等,有一个内角相等的两个等腰三角形 |
20.下列运算中正确的是( )
| A. | 2x+3y=5xy | B. | a3-a2=a | C. | (a-1)(a-2)=a2+a-2 | D. | (a-ab)÷a=1-b |
10.下列运算正确的是( )
| A. | a6÷a2=a4 | B. | a6×a4=a24 | C. | a5+a5=a10 | D. | a4-a4=a0 |
17.下列各组数是无理数的是( )
| A. | 0.2,$\sqrt{3}$ | B. | $\frac{{\sqrt{2}}}{3}$,3 | C. | $3\sqrt{2}$,π | D. | $\sqrt{4}$,1 |
14.下列运算正确的是( )
| A. | (-2)2=-4 | B. | $\sqrt{4}$=2 | C. | 2-3=8 | D. | π0=0 |
15.?ABCD中,如果∠B=120°,那么∠A、∠D的值分别是( )
| A. | ∠A=60°,∠D=120° | B. | ∠A=120°,∠D=60° | C. | ∠A=60°,∠D=60° | D. | ∠A=120°,∠D=120° |
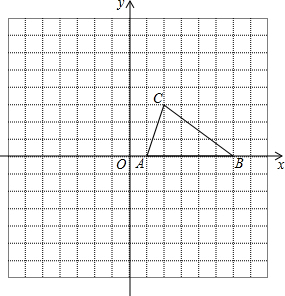 如图方格纸中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(6,0)、C(2,3).
如图方格纸中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(6,0)、C(2,3).