题目内容
2.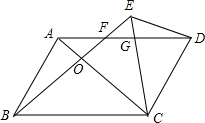 如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)
如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)
分析 利用截长补短进行添加辅助线,①如图1中,在线段EC上截取EM=ED.②如图2中,在线段EC上截取EF=EM.③如图3中,延长FE到M使得EM=ED.④如图4中,延长DE到M,使得EM=EF.
解答  方法一:(截长法).
方法一:(截长法).
证明:如图1中,在线段EC上截取EM=ED.
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,
∵DF=AB=CD,
∴△DFC是等边三角形,
∴CF=CD=DF,∠FCD=∠CFD=∠CDF=60°,
∵∠FEC=∠CDG=60°,
∴E、F、C、D四点共圆,
∴∠DEC=∠CFG=60°,
∴△EDM是等边三角形,
∴∠EDM=∠FDC=60°,ED=EM=DM,
∴∠EDF=∠MDC,
在△EDF和△MDC中,
$\left\{\begin{array}{l}{ED=DM}\\{∠EDF=∠MDC}\\{DF=DC}\end{array}\right.$,
∴△EDF≌△MDC,
∴EF=CM,
∴EC=EM+CM=DE+EF.
方法二:(截长法).
如图2中,在线段EC上截取EF=EM.只要证明△EFD≌△MFC.证明方法类似(1). 方法三:(补短法)
方法三:(补短法)
如图3中,延长FE到M使得EM=ED.
∵∠MED=180°-∠FEC-∠CED=60°,
∴△EMD是等边三角形,
∴EM=ED=DM,∠MDE=∠CDF=60°,
∴∠MDF=∠CDF,
在△MDF和△EDC中,
$\left\{\begin{array}{l}{DM=DE}\\{∠MDF=∠EDC}\\{DF=DC}\end{array}\right.$, ∴△MDF≌△EDC,
∴△MDF≌△EDC,
∴EC=FM=EF+EM=EF+ED.
方法四:(补短法).
如图4中,延长DE到M,使得EM=EF,只要证明△DMF≌△CEF,证明方法类似(3).
点评 本题考查平行四边形的性质、全等三角形的判定和性质、四点共圆等知识,解题的关键是正确添加辅助线,构造特殊三角形,利用全等三角形的性质解决问题,属于中考常考题型.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | $\sqrt{4}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
| A. | a6÷a2=a4 | B. | a6×a4=a24 | C. | a5+a5=a10 | D. | a4-a4=a0 |
| A. | 0.2,$\sqrt{3}$ | B. | $\frac{{\sqrt{2}}}{3}$,3 | C. | $3\sqrt{2}$,π | D. | $\sqrt{4}$,1 |
| A. | 9 | B. | 27 | C. | 6 | D. | 0 |
| A. | (-2)2=-4 | B. | $\sqrt{4}$=2 | C. | 2-3=8 | D. | π0=0 |
| A. | ($\frac{1}{3}$)-1=3 | B. | (-2)3=8 | C. | (a-b)2=a2-b2 | D. | (a2)3÷a3=a2 |
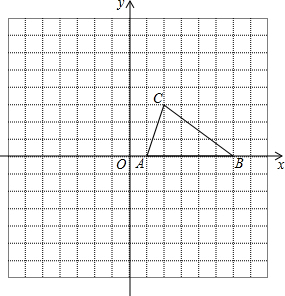 如图方格纸中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(6,0)、C(2,3).
如图方格纸中,已知△ABC的三个顶点的坐标分别为A(1,0)、B(6,0)、C(2,3).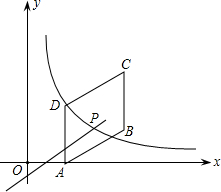 如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论: