题目内容
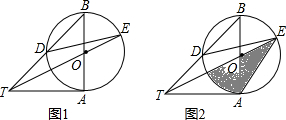
13.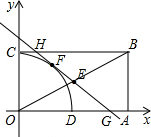 如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H,以O为圆心,OC为半径的圆弧交OA于D,若直线GH与弧CD所在的圆相切于矩形内一点F,则下列结论:①AG=CH;②GH=$\frac{5}{3}$;③直线GH的函数关系式y=-$\frac{3}{4}x+\frac{5}{4}$;④梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,⊙P的半径为$\frac{1}{4}$.其中正确的有( )
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H,以O为圆心,OC为半径的圆弧交OA于D,若直线GH与弧CD所在的圆相切于矩形内一点F,则下列结论:①AG=CH;②GH=$\frac{5}{3}$;③直线GH的函数关系式y=-$\frac{3}{4}x+\frac{5}{4}$;④梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,⊙P的半径为$\frac{1}{4}$.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据矩形性质得到OE=BE,BC∥OA,OA=BC,从判断出△BHE≌△OGE,即可;
②根据矩形的对角线互相平分和圆的切线的性质表示出Rt△MHE中的两边,已知一边,从而求出图形中相关的线段,得到点H,G的坐标,求GH的长,
③由②中得到的点H,G的坐标,利用待定系数法求出直线解析式,
④利用全等三角形,角平分线及圆的切线的性质构造出相似三角形,得出比例式,求出圆的半径.
解答 解:①∵四边形OABC是矩形,
∴OE=BE,BC∥OA,OA=BC,
∴∠HBE=∠GOE,
∵在△BHE和△OGE中,∠HBE=∠GOE,OE=BE,∠HEB=∠GEO,
∴△BHE≌△OGE(ASA),
∴BH=OG,
∴AG=CH.
②如图1,连接DE并延长DE交CB于M,连接AC,则由矩形的性质,点E在AC上.
∵DD=OC=1=$\frac{1}{2}$OA,
∴D是OA的中点,
∵在△CME和△ADE中,
∠MCE=∠DAE,CE=AE,∠MEC=∠DEA,
∴△CME≌△ADE(ASA),
∴CM=AD=2-1=1,
∵BC∥OA,∠COD=90°,
∴四边形CMDO是矩形,
∴MD⊥OD,MD⊥CB,
∴MD切⊙O于D,
∵HG切⊙O于F,E(1,$\frac{1}{2}$),
∴可设CH=HF=x,FE=ED=$\frac{1}{2}$=ME,
在Rt△MHE中,有MH2+ME2=HE2,
即(1-x)2+($\frac{1}{2}$)2=($\frac{1}{2}$+x)2,解得x=$\frac{1}{3}$.
∴H($\frac{1}{3}$,1),OG=2-$\frac{1}{3}$=$\frac{5}{3}$,
∴G($\frac{5}{3}$,0).
∴GH2=($\frac{5}{3}$-$\frac{1}{3}$)2+(0-1)2=$\frac{25}{9}$,
∴GH=$\frac{5}{3}$,
③设直线GH的解析式是:y=kx+b,
把G、H的坐标代入得$\left\{\begin{array}{l}{\frac{5}{3}k+b=0}\\{\frac{1}{3}k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{5}{4}}\end{array}\right.$,
∴直线GH的函数关系式为y=-$\frac{3}{4}$x+$\frac{5}{4}$,
④如图2,连接BG,
∵在△OCH和△BAG中,
CH=AG,∠HCO=∠GAB,OC=AB,
∴△OCH≌△BAG(SAS).
∴∠CHO=∠AGB.
∵∠HCO=90°,
∴HC切⊙O于C,HG切⊙O于F.
∴OH平分∠CHF.
∴∠CHO=∠FHO=∠BGA.
∵△CHE≌△AGE,
∴HE=GE.
∵在△HOE和△GBE中,HE=GE,∠HEO=∠GEB,OE=BE,
∴△HOE≌△GBE(SAS).
∴∠OHE=∠BGE.
∵∠CHO=∠FHO=∠BGA,
∴∠BGA=∠BGE,即BG平分∠FGA.
∵⊙P与HG、GA、AB都相切,
∴圆心P必在BG上.
过P做PN⊥GA,垂足为N,则△GPN∽△GBA.
∴$\frac{PN}{AB}$=$\frac{GN}{AG}$,
设半径为r,则 $\frac{r}{1}=\frac{\frac{1}{3}-r}{\frac{1}{3}}$,解得r=$\frac{1}{4}$.
故选D.
点评 本题是圆的综合题,主要考查了圆中切线的性质和判定,涉及的知识点比较多,如相似三角形的判定和性质,勾股定理,矩形的性质等,解本题的关键是构造出直角三角形和相似三角形,难点是不容易找出求⊙P的半径时的三对全等三角形.

 名校课堂系列答案
名校课堂系列答案| A. | 166×104 | B. | 1.66×105 | C. | 1.66×106 | D. | 0.166×107 |
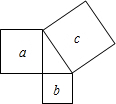 如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )| A. | a+b=c | B. | a2+b2=c2 | C. | ab=c | D. | a+b=c2 |
 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.