题目内容
18.解不等式:$\frac{5x+1}{2}-\frac{x-2}{4}>\frac{5x-1}{6}+\frac{x-3}{3}$.分析 利用不等式的基本性质,即可求得原不等式的解集.
解答 解:去分母得:6(5x+1)-3(x-2)>2(5x-1)+4(x-3),
去括号得:0x+6-3x+6>10x-2+4x-12,
移项得:30x-3x-10x-4x>-2-12-6-6,
合并同类项得:13x>-26,
系数化为1得:x>-13.
点评 本题考查了解一元一次不等式,熟练掌握不等式的性质是解题的关键.

练习册系列答案
相关题目
18.在“百度”搜索中输入“新版中小学生则”,相关结果约1660000个,这个数据可用科学记数法表示为( )
| A. | 166×104 | B. | 1.66×105 | C. | 1.66×106 | D. | 0.166×107 |
13.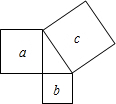 如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
 如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )| A. | a+b=c | B. | a2+b2=c2 | C. | ab=c | D. | a+b=c2 |
7.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
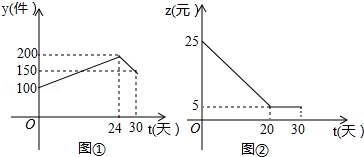

| A. | 第24天的销售量最多 | |
| B. | 20≤t≤30日销售利润不变 | |
| C. | 第30天的日销售利润是750元 | |
| D. | 当0≤t≤24时,设产品日销售量y与时间t的函数关系为y=$\frac{25}{6}$t+100 |
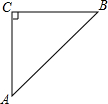 如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.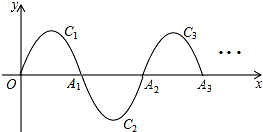 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.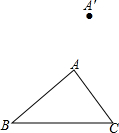 平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.
平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.