题目内容
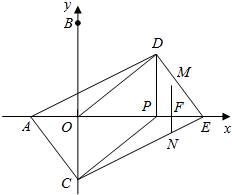
如图,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,6).动点P从点O出发,沿x轴正方向以每 秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中,设?PCOD的面积为S.
①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.
 秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中,设?PCOD的面积为S.
①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.
考点:四边形综合题
专题:几何综合题,压轴题
分析:(1)由C是OB的中点求出时间,再求出点E的坐标,
(2)连接CD交OP于点G,由?PCOD的对角线相等,求四边形ADEC是平行四边形.
(3)当点C在BO上时,第一种情况,当点M在CE边上时,由△EMF∽△ECO求解,第二种情况,当点N在DE边上时,由△EFN∽△EPD求解;
当点C在BO的延长线上时,第一种情况,当点M在DE边上时,由EMF∽△EDP求解,第二种情况,当点N在CE边上时,由△EFN∽△EOC求解;
②当1≤t<
时和当
<t≤5时,分别求出S的取值范围,
(2)连接CD交OP于点G,由?PCOD的对角线相等,求四边形ADEC是平行四边形.
(3)当点C在BO上时,第一种情况,当点M在CE边上时,由△EMF∽△ECO求解,第二种情况,当点N在DE边上时,由△EFN∽△EPD求解;
当点C在BO的延长线上时,第一种情况,当点M在DE边上时,由EMF∽△EDP求解,第二种情况,当点N在CE边上时,由△EFN∽△EOC求解;
②当1≤t<
| 9 |
| 4 |
| 9 |
| 2 |
解答:解:(1)∵OB=6,C是OB的中点,
∴BC=
OB=3,
∴2t=3即t=
,
∴OE=
+3=
,E(
,0);
(2)如图,连接CD交OP于点G,
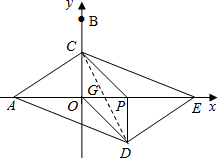
在?PCOD中,CG=DG,OG=PG,
∵AO=PE,
∴AG=EG,
∴四边形ADEC是平行四边形.
(3)①(Ⅰ)当点C在BO上时,
第一种情况:如图,当点M在CE边上时,
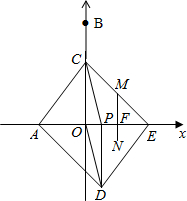
∵MF∥OC,
∴△EMF∽△ECO,
∴
=
,即
=
,
∴t=1,
第二种情况:当点N在DE边时,
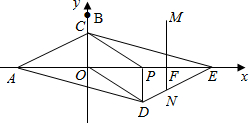
∵NF∥PD,
∴△EFN∽△EPD,
∴
=
,即
=
,
∴t=
,
(Ⅱ)当点C在BO的延长线上时,
第一种情况:当点M在DE边上时,
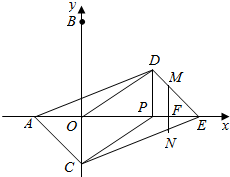
∵MF∥PD,
∴△EMF∽△EDP,
∴
=
即
=
,
∴t=
,
第二种情况:当点N在CE边上时,
∵NF∥OC,
∴△EFN∽△EOC,
∴
=
即
=
,
∴t=5.
②
<S≤
或
<S≤20.
当1≤t<
时,
S=t(6-2t)=-2(t-
)2+
,
∵t=
在1≤t<
范围内,
∴
<S≤
,
当
<t≤5时,S=t(2t-6)=2(t-
)2-
,
∴
<S≤20.
∴BC=
| 1 |
| 2 |
∴2t=3即t=
| 3 |
| 2 |
∴OE=
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
(2)如图,连接CD交OP于点G,

在?PCOD中,CG=DG,OG=PG,
∵AO=PE,
∴AG=EG,
∴四边形ADEC是平行四边形.
(3)①(Ⅰ)当点C在BO上时,
第一种情况:如图,当点M在CE边上时,

∵MF∥OC,
∴△EMF∽△ECO,
∴
| MF |
| CO |
| EF |
| EO |
| 2 |
| 6-2t |
| 2 |
| 3+t |
∴t=1,
第二种情况:当点N在DE边时,

∵NF∥PD,
∴△EFN∽△EPD,
∴
| FN |
| PD |
| EF |
| EP |
| 1 |
| 6-2t |
| 2 |
| 3 |
∴t=
| 9 |
| 4 |
(Ⅱ)当点C在BO的延长线上时,
第一种情况:当点M在DE边上时,

∵MF∥PD,
∴△EMF∽△EDP,
∴
| MF |
| DP |
| EF |
| EP |
| 2 |
| 2t-6 |
| 2 |
| 3 |
∴t=
| 9 |
| 2 |
第二种情况:当点N在CE边上时,

∵NF∥OC,
∴△EFN∽△EOC,
∴
| FN |
| OC |
| EF |
| EO |
| 1 |
| 2t-6 |
| 2 |
| 3+t |
∴t=5.
②
| 27 |
| 8 |
| 9 |
| 2 |
| 27 |
| 2 |
当1≤t<
| 9 |
| 4 |
S=t(6-2t)=-2(t-
| 3 |
| 2 |
| 9 |
| 2 |
∵t=
| 3 |
| 2 |
| 9 |
| 4 |
∴
| 27 |
| 8 |
| 9 |
| 2 |
当
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
∴
| 27 |
| 2 |
点评:本题主要是考查了四边形的综合题,解题的关键是正确分几种不同种情况求解.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
| A、矩形 |
| B、等腰梯形 |
| C、对角线相等的四边形 |
| D、对角线互相垂直的四边形 |
 如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出一组相似的三角形:
如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出一组相似的三角形: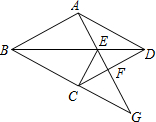 如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.
如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.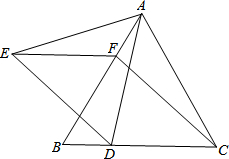 如图,等边△ABC中,D、F分别是边BC、AB上的点,且CD=BF,以AD为边向左作等边△ADE,连接CF、EF,设BD:DC=K.
如图,等边△ABC中,D、F分别是边BC、AB上的点,且CD=BF,以AD为边向左作等边△ADE,连接CF、EF,设BD:DC=K. 如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.
如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.
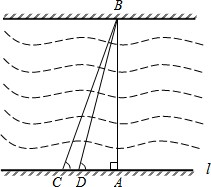 “中国-益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
“中国-益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).