题目内容
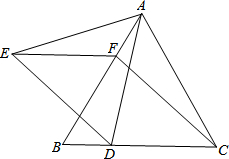 如图,等边△ABC中,D、F分别是边BC、AB上的点,且CD=BF,以AD为边向左作等边△ADE,连接CF、EF,设BD:DC=K.
如图,等边△ABC中,D、F分别是边BC、AB上的点,且CD=BF,以AD为边向左作等边△ADE,连接CF、EF,设BD:DC=K.(1)求证:△ACD≌△CBF;
(2)判断四边形CDEF是怎样的特殊四边形,并说明理由;
(3)当∠DEF=45°时,求k的值.
考点:全等三角形的判定与性质,等边三角形的性质,平行四边形的判定与性质
专题:常规题型
分析:(1)△ABC为等边三角形,则可证明△ACD≌△CBF;
(2)根据△ACD≌△CBF可得AD=CF,即而可证ED∥CF,可得四边形CDEF是平行四边形;
(3)易证CH=
n,DH=
n,再根据AH=DH即可求出k的值.
(2)根据△ACD≌△CBF可得AD=CF,即而可证ED∥CF,可得四边形CDEF是平行四边形;
(3)易证CH=
| 1 |
| 2 |
| ||
| 2 |
解答:解:(1)∵△ABC是等边三角形,
∴AC=CB,∠ACB=∠B=60°,
又∵CD=BF,
∴△ACD≌△CBF;
(2)由(1)得△ACD≌△CBF,
∴∠CAD=∠BCF,AD=CF
又∵△ADE是等边三角形,
∴ED=AD=CF,∠EDA=60°,
∵∠BDA=∠BDE+∠EDA=∠CAD+60°,
∴∠BDE=∠CAD=∠BCF,
∴ED∥CF,
∴四边形CDEF是平行四边形.
(3)过D点作DH⊥AC垂足为H,

∵BD:DC=K,∴设BD=nK,DC=n
∵∠ACB=60°,
∴∠HDC=30°,
∴CH=
n,DH=
n
∵四边形CDEF是平行四边形,
∴∠DEF=∠DCF=∠CAD=45°
∴∠ADH=∠HAD=45°,
∴AH=DH=
n,
∴nk+n=
n+
n,
∴k=
+
-1=
.
∴AC=CB,∠ACB=∠B=60°,
又∵CD=BF,
∴△ACD≌△CBF;
(2)由(1)得△ACD≌△CBF,
∴∠CAD=∠BCF,AD=CF
又∵△ADE是等边三角形,
∴ED=AD=CF,∠EDA=60°,
∵∠BDA=∠BDE+∠EDA=∠CAD+60°,
∴∠BDE=∠CAD=∠BCF,
∴ED∥CF,
∴四边形CDEF是平行四边形.
(3)过D点作DH⊥AC垂足为H,

∵BD:DC=K,∴设BD=nK,DC=n
∵∠ACB=60°,
∴∠HDC=30°,
∴CH=
| 1 |
| 2 |
| ||
| 2 |
∵四边形CDEF是平行四边形,
∴∠DEF=∠DCF=∠CAD=45°
∴∠ADH=∠HAD=45°,
∴AH=DH=
| ||
| 2 |
∴nk+n=
| 1 |
| 2 |
| ||
| 2 |
∴k=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查了等边三角形的性质,考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质.

练习册系列答案
相关题目
反比例函数y=-
(x>0),点B为其上一点,点A为x轴负半轴上一点,当点B的横坐标逐渐减小时,△AOB的面积( )
| 2 |
| x |
| A、逐渐减少 | B、逐渐增大 |
| C、不变 | D、先增大后减小 |
 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 如图,在Rt△ABC中,M、N是两直角边上的点,且AM=BC,CM=BN,BM、AN交于点P,则∠APM的度数为
如图,在Rt△ABC中,M、N是两直角边上的点,且AM=BC,CM=BN,BM、AN交于点P,则∠APM的度数为 秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
 如图,四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F,垂足分别为E、F.
如图,四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F,垂足分别为E、F.