题目内容
若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（ ）
| A、矩形 |
| B、等腰梯形 |
| C、对角线相等的四边形 |
| D、对角线互相垂直的四边形 |
考点：中点四边形
专题：
分析：首先根据题意画出图形，由四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，利用三角形中位线的性质与菱形的性质，即可判定原四边形一定是对角线相等的四边形．
解答：
解：如图，根据题意得：四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，
∴EF=FG=CH=EH，BD=2EF，AC=2FG，
∴BD=AC．
∴原四边形一定是对角线相等的四边形．
故选：C．
解：如图，根据题意得：四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，∴EF=FG=CH=EH，BD=2EF，AC=2FG，
∴BD=AC．
∴原四边形一定是对角线相等的四边形．
故选：C．
点评：此题考查了菱形的性质与三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
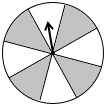有一个能自由转动的转盘如图，盘面被分成8个大小与性状都相同的扇形，颜色分为黑白两种，将指针的位置固定，让转盘自由转动，当它停止后，指针指向白色扇形的概率是
如图，在Rt△ABC中，M、N是两直角边上的点，且AM=BC，CM=BN，BM、AN交于点P，则∠APM的度数为
如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是反比例函数y=-
（x＞0），点B为其上一点，点A为x轴负半轴上一点，当点B的横坐标逐渐减小时，△AOB的面积（ ）
| 2 |
| x |
| A、逐渐减少 | B、逐渐增大 |
| C、不变 | D、先增大后减小 |
秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造?PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．
如图，四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F，垂足分别为E、F．