题目内容
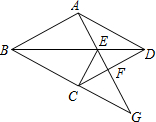 如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.
如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.(1)猜想EC与AE的数量关系为
(2)若F为CD的中点,猜想
| FG |
| EF |
(3)若AE=mEF(m>1),猜想
| FG |
| EF |
考点:相似三角形的判定与性质,全等三角形的判定与性质,菱形的性质
专题:
分析:(1)由菱形的性质可知∠ABE=∠CBE,AB=BC,所以△ABE≌△CBE,所以EC=AE.
(2)通过△ABE∽△FDE即可求得
=3.
(3)由(2)可知
=m2-1.
(2)通过△ABE∽△FDE即可求得
| FG |
| EF |
(3)由(2)可知
| FG |
| EF |
解答:解:(1)EC与AE的数量关系为EC=AE.
(2)3,
理由:∵四边形ABCD为菱形,
∴AD∥CG,
∴∠DAF=∠G,
又∵F为CD的中点,
∴DF=FG,
又∵∠AFD=∠GFC,
在△ADF与△GCF中,
,
∴△ADF≌△GCF(AAS)
∴AF=FG,
由四边形ABCD为菱形,可得AB=CD=2FD,AB∥DF,
∴△ABE∽△FDE,
∴
=
=
,即AE=2EF,
∴FG=AF=3EF,
∴
=3.
(3)m2-1.
故答案为EC=AE,3,m2-1.
(2)3,
理由:∵四边形ABCD为菱形,
∴AD∥CG,
∴∠DAF=∠G,
又∵F为CD的中点,
∴DF=FG,
又∵∠AFD=∠GFC,
在△ADF与△GCF中,
|
∴△ADF≌△GCF(AAS)
∴AF=FG,
由四边形ABCD为菱形,可得AB=CD=2FD,AB∥DF,
∴△ABE∽△FDE,
∴
| FD |
| AB |
| EF |
| AE |
| 1 |
| 2 |
∴FG=AF=3EF,
∴
| FG |
| EF |
(3)m2-1.
故答案为EC=AE,3,m2-1.
点评:此题主要考查菱形的性质及相似三角形的判定定理及性质.

练习册系列答案
相关题目
下列实数中是无理数的是( )
A、
| ||||
| B、2-2 | ||||
C、5.
| ||||
| D、sin45° |
 如图,△ABC内接于⊙O,AO=2,BC=2
如图,△ABC内接于⊙O,AO=2,BC=2 如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是
如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒. (1)已知反比例函数y=
(1)已知反比例函数y=