题目内容
7.已知关于x的一元二次方程kx2-(4k+1)x+3k+3=0(k是整数).(1)求证:无论k为何值,方程总有两个不相等的实数根;
(2)若方程的两个不等的实数根分别为x1、x2(其中x1<x2),设y=$\frac{1}{3}{x}_{2}-{x}_{1}$,判断y是否为k的函数?如果是,请写出函数关系式;若不是,请说明理由.
分析 (1)分类讨论:当k=0时,方程为以元一次方程,有解;当k≠0时,根据计算配不上得到△=(2k-1)2≥0,则可判断方程有两个实数解;
(2)利用求根公式得到x1=1+$\frac{1}{k}$,x2=3,则y=1-(1+$\frac{1}{k}$)=-$\frac{1}{k}$,于是可判断y是k的反比例函数.
解答 (1)证明:当k=0时,方程变形为-x+3=0,解得x=3;
当k≠0时,△=(4k+1)2-4k•(3k+3)=(2k-1)2≥0,方程有两个实数解,
所以不论k为何值,方程总有实数根;
(2)根据题意得x=$\frac{4k+1±(2k-1)}{2k}$,
所以x1=$\frac{k+1}{k}$=1+$\frac{1}{k}$,x2=3,
所以y=1-(1+$\frac{1}{k}$)=-$\frac{1}{k}$,
所以y是k的反比例函数.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
15.2-1等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
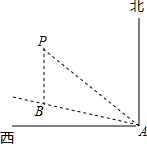 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?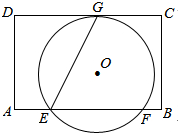 如图,在矩形ABCD中,AD=8,E是AB边上一点,且AE=$\frac{1}{4}$AB,⊙O经过点E,若⊙O与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在射线相交于另一点F,且EG:EF=$\sqrt{5}$:2.
如图,在矩形ABCD中,AD=8,E是AB边上一点,且AE=$\frac{1}{4}$AB,⊙O经过点E,若⊙O与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在射线相交于另一点F,且EG:EF=$\sqrt{5}$:2. 如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )
如图,在一块△ABC板面中,将△BEF涂黑,其中点D、E、F分别为BC、AD、CE的中点,小华随意向△ABC板面内部射击一粒小弹丸,则弹丸击中黑色区域的概率是( )