题目内容
12.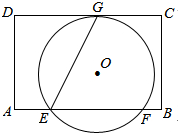 如图,在矩形ABCD中,AD=8,E是AB边上一点,且AE=$\frac{1}{4}$AB,⊙O经过点E,若⊙O与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在射线相交于另一点F,且EG:EF=$\sqrt{5}$:2.
如图,在矩形ABCD中,AD=8,E是AB边上一点,且AE=$\frac{1}{4}$AB,⊙O经过点E,若⊙O与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在射线相交于另一点F,且EG:EF=$\sqrt{5}$:2.(1)求⊙O的半径r;
(2)当边AD或BC所在直线与⊙O相切时,直接写出AE的长;以及⊙O与矩形ABCD边的公共点个数.
分析 (1)连接GO并延长交AB于点H,由切线的性质易得HG⊥CD,由矩形的性质易证得四边形AHGD为矩形,设EG=$\sqrt{5}$m,则EH=m,在Rt△GEH中,由勾股定理易得m,即得EH的长,在Rt△OEH中,由勾股定理可得r的长;
(2)当⊙O与AD相切时,由切线的性质和半径可得AE=1,求出AB的边长可得交点个数;当⊙O与BC相切时,同理可得,此时AE=3,求出AB的边长可得交点个数.
解答 解:(1)连接GO并延长交AB于点H,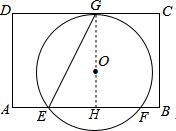
∵CD与⊙O相切于点G,
∴HG⊥CD,
∵四边形ABCD为矩形,
∴AB∥CD,
∴GH⊥AB,
即GH⊥EF,
∴EH=HF=$\frac{1}{2}EF$,
∵矩形ABCD中,AD=8,
∴∠D=∠A=∠AHG=90°,
∴四边形AHGD为矩形,GH=AD=8,
∴在Rt△GEH中,EG:EF=$\sqrt{5}$:2,
设EG=$\sqrt{5}$m,则EH=m,
∴EG2-EH2=GH2,
则m=±4,EH=4,
在Rt△OEH中,由勾股定理得r2=42+(8-r)2,
解得:r=5;
(2)当⊙O与AD相切时,此时AE=AH-EH=r-EH=5-4=1,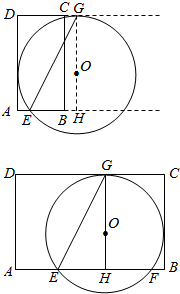
∵AE=$\frac{1}{4}$AB,
∴AB=4,
∴⊙O与矩形ABCD边有3个公共点,如图所示;
当⊙O与BC相切时,
∵EH=4,BH=r=5,
∴BE=4+5=9,
∵AE=$\frac{1}{4}$AB,
∴BE=$\frac{3}{4}$AB,
∴AB=12,
∴AE=3.
∴⊙O与矩形ABCD边有4个公共点,如图所示.
点评 此题主要考查了切线的性质,连接圆心和切点,作出恰当的辅助线是解答此题的关键.

练习册系列答案
相关题目
3.若a<b<0,化简$\root{3}{{{{({a-b})}^3}}}-\sqrt{{{({a-b})}^2}}+\root{3}{a^3}-\sqrt{b^2}$的结果为( )
| A. | 3a-b | B. | 3(b-a) | C. | a-b | D. | b-a |
4.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{2a}$ | B. | $\sqrt{\frac{b}{3}}$ | C. | $\sqrt{{c}^{3}}$ | D. | $\sqrt{8{d}^{2}}$ |
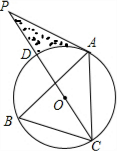 如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.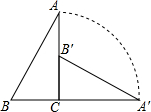 如图,已知△ABC中∠A=30°,∠C=90°,AB=4,将△ABC绕点C顺时针旋转90°得到△A′B′C′.在整个旋转过程中.
如图,已知△ABC中∠A=30°,∠C=90°,AB=4,将△ABC绕点C顺时针旋转90°得到△A′B′C′.在整个旋转过程中.