如图所示.在平行四边形ABCD中.过点B作BE⊥CD.垂足为E.连接AE.F为AE上的一点.且∠BFE=∠C.求证:△ABF∽△EAD．题目和参考答案——青夏教育精英家教网—

题目内容

10．

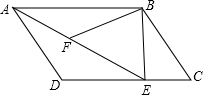如图所示，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上的一点，且∠BFE=∠C，求证：△ABF∽△EAD．

分析由四边形ABCD是平行四边形，可证得∠C+∠D=180°，∠BAF=∠AED，又由∠BFE=∠C，易得∠AFB=∠D，即可证得：△ABF∽△EAD．

解答解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
∴∠C+∠D=180°，∠BAF=∠AED，
∵∠AFB+∠BFE=180°，∠BFE=∠C，
∴∠AFB=∠D，
∴△ABF∽△EAD．

点评此题考查了相似三角形的判定以及平行四边形的性质．注意有两组角对应相等的两个三角形相似．

练习册系列答案

相关题目

1．若3cm、4cm、xcm能构成一个直角三角形，则x=（　　）

18．等腰三角形的边长分别为6和8，则底角余弦值为$\frac{2}{3}$或$\frac{3}{8}$．

5．命题：①“对顶角相等”的逆命题一定是真命题；②垂直于同一条直线的两直线平行；③如果一个三角形中有两边的平方和等于第三边的平方，那么这个三角形是直角三角形；④同位角相等．其中假命题有（　　）

15．阅读下列解题过程：
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{1×（\sqrt{4}-\sqrt{3}）}{（\sqrt{4}+\sqrt{3}）（\sqrt{4}-\sqrt{3}）}$=$\frac{\sqrt{4}-\sqrt{3}}{（\sqrt{4}）^{2}-（\sqrt{3}）^{2}}$=$\sqrt{4}$-$\sqrt{3}$=2-$\sqrt{3}$；
$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\frac{1×（\sqrt{5}-\sqrt{4}）}{（\sqrt{5}+\sqrt{4}）（\sqrt{5}-\sqrt{4}）}$=$\frac{\sqrt{5}-\sqrt{4}}{（\sqrt{5}）^{2}-（\sqrt{4}）^{2}}$=$\sqrt{5}$-$\sqrt{4}$=$\sqrt{5}$-2；
请回答下列问题：
（1）观察上面的解题过程，请直接写出式子：$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$；（n≥1）
（2）利用上面所提供的解法，请化简：
$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+$\frac{1}{\sqrt{5}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$的值．

2．给出下列关于$\sqrt{2}$的判断：㈠$\sqrt{2}$是无理数；㈡$\sqrt{2}$是实数；㈢$\sqrt{2}$是2的算术平方根；㈣1＜$\sqrt{2}$＜2．其中正确的是（　　）

19．

如图，点A、B、C都在⊙O上，如果∠AOB=84°，那么∠ACB的大小是42°．

20．某超市一月份的营业额为100万元，三月份的营业额为144万元，如果每月比上月增长的百分数相同，则平均每月的增长率为（　　）

试题分类