题目内容
15.阅读下列解题过程:$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{1×(\sqrt{4}-\sqrt{3})}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4})^{2}-(\sqrt{3})^{2}}$=$\sqrt{4}$-$\sqrt{3}$=2-$\sqrt{3}$;
$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\frac{1×(\sqrt{5}-\sqrt{4})}{(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})}$=$\frac{\sqrt{5}-\sqrt{4}}{(\sqrt{5})^{2}-(\sqrt{4})^{2}}$=$\sqrt{5}$-$\sqrt{4}$=$\sqrt{5}$-2;
请回答下列问题:
(1)观察上面的解题过程,请直接写出式子:$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;(n≥1)
(2)利用上面所提供的解法,请化简:
$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+$\frac{1}{\sqrt{5}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$的值.
分析 (1)根据观察,可得规律$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;
(2)根据规律,可简便运算.
解答 解:(1)$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;
故答案是:$\sqrt{n}$-$\sqrt{n-1}$;
(2)原式=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}$-$\sqrt{3}$)+($\sqrt{5}$-$\sqrt{4}$)+…+($\sqrt{2013}$-$\sqrt{2012}$)
=$\sqrt{2013}$-1.
点评 本题考查了分母有理化,利用了平方差公式进行分母有理化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.水库管理人员为掌握水库蓄水情况,需要观测水库水位变化,下表是一周内水位高低的变化情况,用正数表示水位比前一天上升数,用负数表示水位比前一天下降数.
(1)问水库的水位在本周内是上升还是下降,幅度是多少米?
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 水位变化(米) | 0.12 | -0.02 | -0.13 | -0.20 | -0.08 | -0.02 | 0.32 |
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
 如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.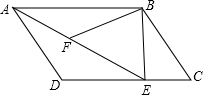 如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.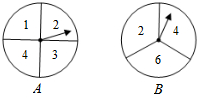 如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y). 已知:如图所示,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交AB于点F.求证:∠D=∠AFD.
已知:如图所示,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交AB于点F.求证:∠D=∠AFD.