题目内容
18．等腰三角形的边长分别为6和8，则底角余弦值为$\frac{2}{3}$或$\frac{3}{8}$．分析 如图，AB=AC，作AD⊥BC于D，根据等腰三角形的性质得BD=CD，然后分类讨论：当AB=AC=6，BC=8时，BD=4，然后在Rt△ABD中利用正切的定义求解；当AB=AC=8，BC=6时，BD=3，然后在Rt△ABD中利用正切的定义求解．
解答 解：
如图，AB=AC，作AD⊥BC于D，则BD=CD，
当AB=AC=6，BC=8时，BD=4，在Rt△ABD中，tanB=$\frac{BD}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$；
当AB=AC=8，BC=6时，BD=3，在Rt△ABD中，tanB=$\frac{BD}{AB}$=$\frac{3}{8}$，
所以等腰三角形底角的余弦值为$\frac{2}{3}$或$\frac{3}{8}$．
故答案为$\frac{2}{3}$或$\frac{3}{8}$．
点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了等腰三角形的性质．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
如图所示的一块地ABCD，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，求这块地的面积．
小惠同学学习了轴对你知识后，忽然想起了过去做过的一道题：有一组数排列成方阵，如图所示，试计算这组数的和，小惠想方阵就像小正方形，正方形是轴对称图形，能不能利用轴对称的思想来解决方阵的问题呢？小惠试了试，竟得到了非常巧妙的方法．请你试试看!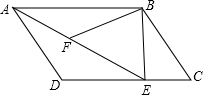
如图所示，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上的一点，且∠BFE=∠C，求证：△ABF∽△EAD．