题目内容
10.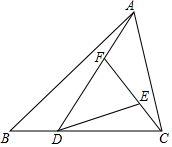 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
分析 根据共高的两三角形的面积比等于底边的比分别求出S△ACD、S△CDF、S△DEF,可得答案.
解答 解:∵BD=$\frac{1}{2}$DC,
∴CD=$\frac{2}{3}$BC,
∴S△ACD=$\frac{2}{3}$S△ABC=$\frac{2}{3}$,
又∵AF=$\frac{1}{2}$FD,即DF=$\frac{2}{3}$AD,
∴S△CDF=$\frac{2}{3}$S△ACD=$\frac{4}{9}$,
∵CE=$\frac{1}{2}$EF,即EF=$\frac{2}{3}$CF,
∴S△DEF=$\frac{2}{3}$S△CDF=$\frac{8}{27}$.
故选D.
点评 本题主要考查三角形的面积,掌握共高的两三角形的面积比等于底边的比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设a=$\sqrt{2012}$+$\sqrt{2008}$,b=$\sqrt{2013}$+$\sqrt{2007}$,c=$\sqrt{2014}$+$\sqrt{2006}$,则a,b,c之间的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | a<c<b |
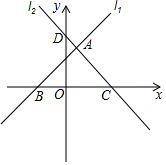 如图所示,在平面直角坐标系中,直线l1:y=x+1与l2:y=-x+2分别交x轴于点B和点C,点D是直线l2与y轴的交点,两直线交于点A.
如图所示,在平面直角坐标系中,直线l1:y=x+1与l2:y=-x+2分别交x轴于点B和点C,点D是直线l2与y轴的交点,两直线交于点A.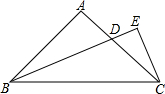 如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于点D,CE⊥BD的延长线于点E,求证:BD=2CE.
如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于点D,CE⊥BD的延长线于点E,求证:BD=2CE.