题目内容
15.计算:(1)$\sqrt{72}$×$\sqrt{\frac{1}{12}}$=$\sqrt{6}$;
(2)(-3$\sqrt{\frac{1}{2}}$)(-4$\sqrt{8}$)=24;
(3)$\frac{4}{3}$$\sqrt{24}$×$\sqrt{6}$=16.
分析 (1)直接利用二次根式的性质化简求出答案;
(2)直接利用二次根式的乘法运算法则化简求出答案;
(3)直接利用二次根式的乘法运算法则化简求出答案.
解答 解:(1)$\sqrt{72}$×$\sqrt{\frac{1}{12}}$=$\sqrt{72×\frac{1}{12}}$=$\sqrt{6}$;
故答案为:$\sqrt{6}$;
(2)(-3$\sqrt{\frac{1}{2}}$)(-4$\sqrt{8}$)=3×4$\sqrt{\frac{1}{2}×8}$=24;
故答案为:24;
(3)$\frac{4}{3}$$\sqrt{24}$×$\sqrt{6}$=$\frac{4}{3}$×$\sqrt{24×6}$=$\frac{4}{3}$×12=16.
故答案为:16.
点评 此题主要考查了二次根式的乘法运算,正确化简二次根式是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
3.y=$\sqrt{x-3}$+$\sqrt{3-x}$+8,则3x+2y的平方根是( )
| A. | 5 | B. | -5 | C. | ±3 | D. | ±5 |
10.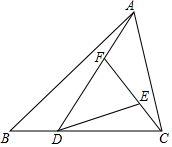 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
20.把4$\sqrt{2\frac{3}{4}}$根号外的因式移进根号内,结果等于( )
| A. | -$\sqrt{11}$ | B. | $\sqrt{11}$ | C. | -$\sqrt{44}$ | D. | $\sqrt{44}$ |
7.与A(a,b)是反比例函数y=$\frac{k}{x}$上的一点,且a,b是关于x的一元二次方程x2-mx+5=0的两根,则反比例函数的解析式为( )
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{x}$ | C. | y=$\frac{5}{x}$ | D. | y=-$\frac{5}{x}$ |
7.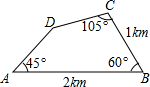 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )| A. | $\frac{3+\sqrt{6}}{4}$km2 | B. | $\frac{3-\sqrt{6}}{4}$km2 | C. | $\frac{6+\sqrt{3}}{4}$km2 | D. | $\frac{6-\sqrt{3}}{4}$km2 |